입체도형의 겉넓이는
입체도형의 전개도를 이용하면
쉽게 구할 수 있다.
여기서, 전개도란
3차원 입체를 2차원 평면으로
펼쳐서 그린 도형을 말한다.
전개도는 입체도형의 모서리를
잘라서 펼친 모양인데
잘린 모서리는 실선으로,
잘리지 않은 모서리는 점선으로 표기하며
모든 면은 적어도 하나 이상의 면과
연결되어 있어야 한다.
[기둥의 겉넓이]

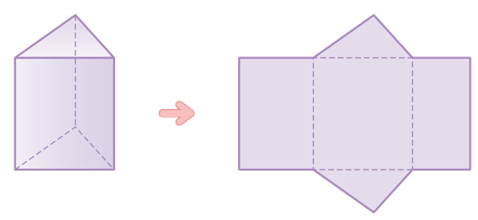
각기둥과 같은 다면체는
모서리를 적절하게 잘라서
펼치면 전개도 완성!
여러가지 모양의 전개도가
나올 수 있으나
겉넓이의 구조를 파악하기에는
위의 전개도가 가장~깔끔하다.
원기둥은 어떨까?
원기둥은 회전체이다.
원 모양의 두 밑면과
모선(옆면을 만드는 선분)이
만들어내는 옆면으로 구성되어 있다.
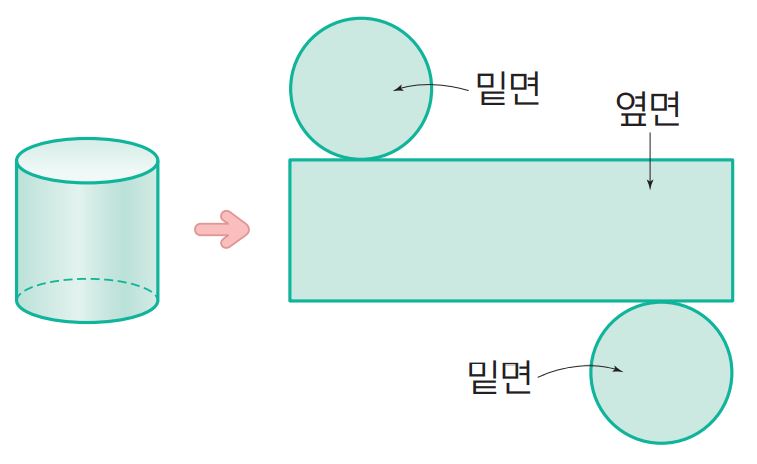
원기둥을 2차원 평면으로 펼치려면
밑면의 원의 경계를 잘라내고
옆면은 모서리 대신
'모선'을 따라 잘라야 한다.
즉, 기둥의 전개도는
합동인 밑면 2개와
직사각형 모양의 옆면 1개로
구성되어 있으며
직사각형인 옆면의 가로의 길이는
밑면을 둘러싸야 하므로
밑면의 둘레의 길이가 될 것이다.
따라서, 기둥의 겉넓이는
(밑넓이)×2 + (옆넓이) 이다.
기둥의 겉넓이를 직접 구해보자.
(1) 삼각기둥
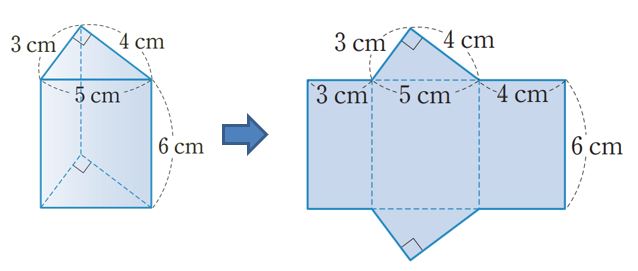
밑넓이 = 3×4×1/2 = 6 (㎠)
옆넓이 = (3+5+4)×6 = 72 (㎠)
겉넓이 = 6×2 + 72 =84 (㎠)
(2) 원기둥
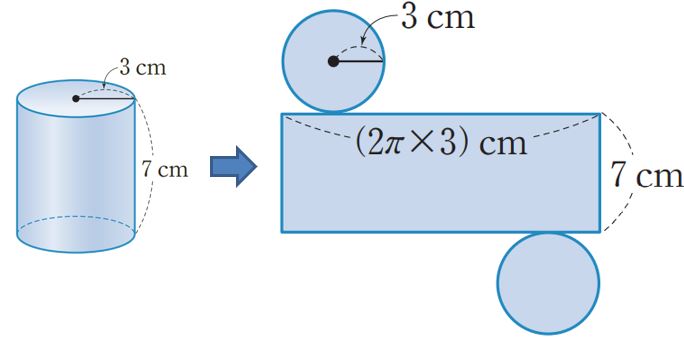
밑넓이 = 9π (㎠)
옆넓이 = 6π × 7 =42π (㎠)
겉넓이 = 9π × 2 + 42π = 60π (㎠)
[뿔의 겉넓이]
뿔에는 각뿔과 원뿔이 있는데
먼저 각뿔의 전개도부터 살펴보자.
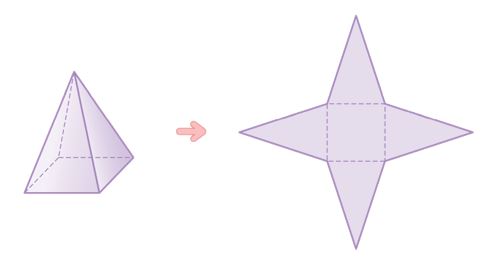
옆면의 모서리를 잘라서 펼치면
사각뿔의 전개도는 아래와 같고
삼각뿔의 전개도는 아래와 같다.
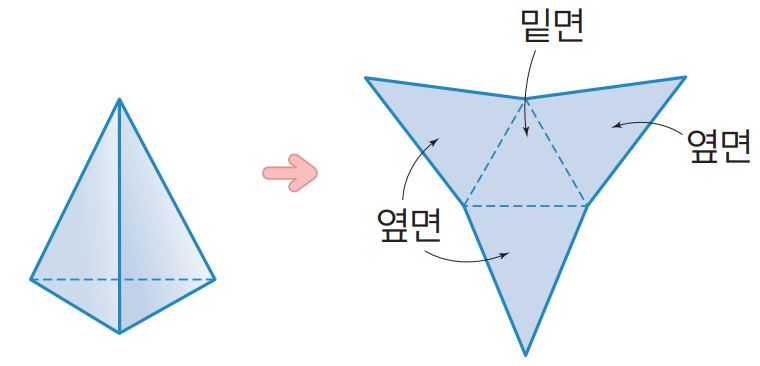
따라서, 각뿔의 겉넓이는
(밑넓이)+(옆넓이)이다.
아래 각뿔의 겉넓이를 구해보자.
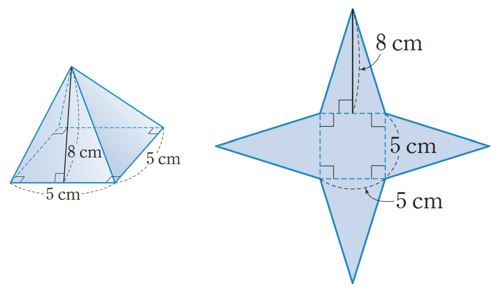
밑넓이 = 25 ㎠
옆넓이 = (5 × 8 × 1/2) ×4 = 80 ㎠
겉넓이 = 25+80 = 105 ㎠ 이다.
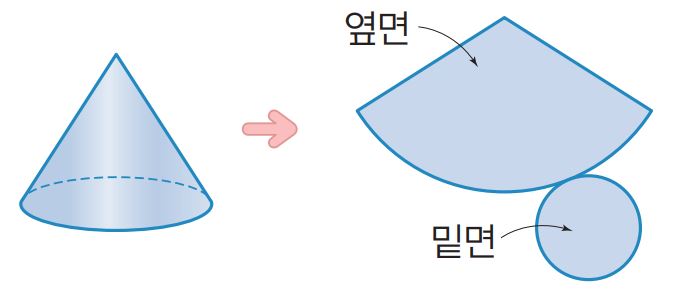
이번에는 원뿔을
2차원 평면에 펼쳐서
전개도를 만들어보자.
밑면의 원의 경계를 잘라내고
모서리 대신
옆면을 구성하는 모선을 따라 잘라낸다.
그러면 아래와 같은 전개도가 등장!
그런데 여기서 잠깐!!
학생들의 대표적인 오답을 살펴보자.
각 반에 몇 명이
원뿔의 전개도를 아래와 같이 그린다.
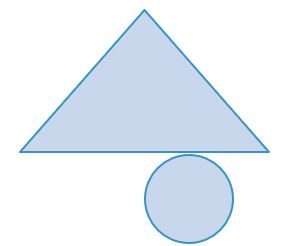
원뿔의 꼭짓점에서
밑면인 원의 경계까지 닿는 모선의 길이는
항상 같기 때문에
옆면을 펼쳤을 때에는
원뿔의 꼭짓점을 중심으로 하고
모선의 길이를 반지름으로 하는
원의 일부(부채꼴)가 나와야 한다.
즉, 원뿔의 겉넓이
= (밑넓이) + (옆넓이)
= (원의 넓이) + (부채꼴의 넓이)
= (밑면의 반지름의 제곱)π +
(1/2×모선의 길이×밑면 원의 둘레)
아래 원뿔의 겉넓이를 구해보자.
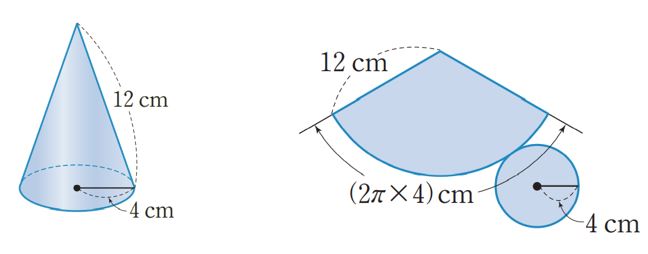
밑넓이 = 16π (㎠)
옆넓이 = 1/2×부채꼴 반지름×부채꼴 호의 길이
=1/2 ×12 × 8π=48π (㎠)
겉넓이 = 16π + 48 π = 64 π (㎠)
[구의 겉넓이]
아래 구의 전개도를 그려보자.

기둥, 뿔의 겉넓이를 구하는 과정과 같이
학생들에게 구의 전개도를
공책에 그려보라고 하면
서로를 쳐다보면서 당황해한다.
구의 전개도는 없지 않나요?라는
질문을 하는 학생도 있다.
그런 아이들에게 아래 그림을 제시해 준다.
구의 표면을 아~주 얇게 썰어서 붙이면
전개도가 되지 않을까?

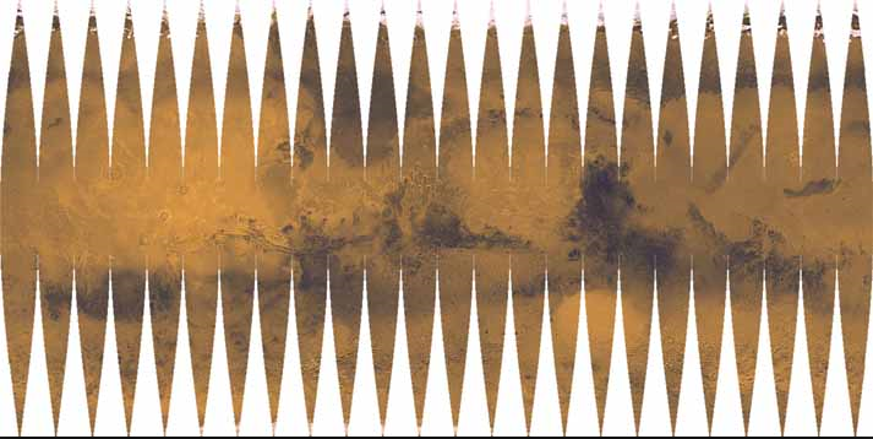

이 그림을 보고 나면
'아하~구도 전개도가 있구나'라고 말하는
학생들도 있다.
그때!!!
전개도의 정의를 다시 상기시켜 주어야 한다.
전개도란,
3차원 입체를 2차원 평면으로 펼친 것!
그런데 구는
모든 점에서 일정하게 구부러져 있다.
즉, 아무리 잘게 쪼갠다고 하더라도
구의 표면을 평면으로 나타낼 수는 없다.
즉, 구는 전개도가 없다.
그렇다면 전개도가 없는
구의 겉넓이는 어떻게 구할까?
중1 수준에서는 구의 겉넓이 공식을
엄밀하게 전개할 수는 없다.
실험을 통해 알아보자.
수업시간에 학생들에게 보여주는 영상이 있다.
EBS MATH > 중학수학 > 중학교1학년
> 기하 > 입체도형의 겉넓이 > 콘텐츠 유형:영상
영상제목 : 구를 구하다
https://www.ebsmath.co.kr/url/go/107957
내용은 다음과 같다.




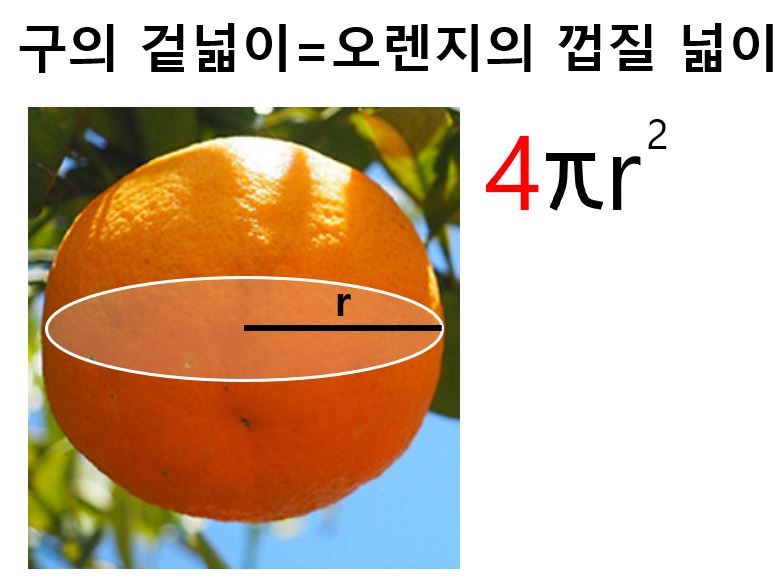
위의 활동에서 오렌지 껍질의 넓이가
구의 겉넓이에 해당한다.
구의 반지름의 길이를 r이라고 하면
구의 대원(구의 중심을 지나게 자른 원)의 넓이는
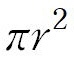
, 영상에서 확인했듯이
구의 겉넓이는 구의 대원의 넓이의 4배가 되므로

문제를 풀어보자.
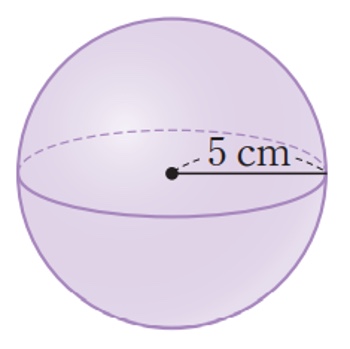
아래 구의 겉넓이는 4 × π × 5 × 5=100 π (㎠)이다.
-삽화 출처 : 천재교육 중학교 수학1 교과서(류희찬)-

적분법을 응용하여
구의 겉넓이와 부피를 구하는 과정은
따로 정리해보도록 하겠다^^!!
'수학 이야기 > 중1수학' 카테고리의 다른 글
| [입체도형]기둥, 뿔, 구의 부피 구하는 방법 (2) | 2023.01.09 |
|---|---|
| [심화]구의 부피, 구의 겉넓이 공식 유도(적분법의 응용, 고등과정) (3) | 2023.01.07 |
| [입체도형]정다면체(정다면체란?, 정다면체 그리는 방법) (0) | 2022.12.29 |
| [입체도형]다면체(각기둥, 각뿔, 각뿔대) (2) | 2022.12.28 |
| [평면도형]다각형의 대각선의 개수 (0) | 2022.12.09 |



