중1 과정에서는 실험을 통해
구의 부피와, 구의 겉넓이 공식을
유도했다.
이는 엄밀한 방법은 아니다.
수학적 호기심을 가지고
구의 부피와 겉넓이를 구하는 방법을
궁금해하는
반에 한 명 있을까 말까한 학생들을 위해
이 글을 써본다.^^
도형의 넓이를 구하기 위해
꼭 알아야 할 내용을 살펴보자.
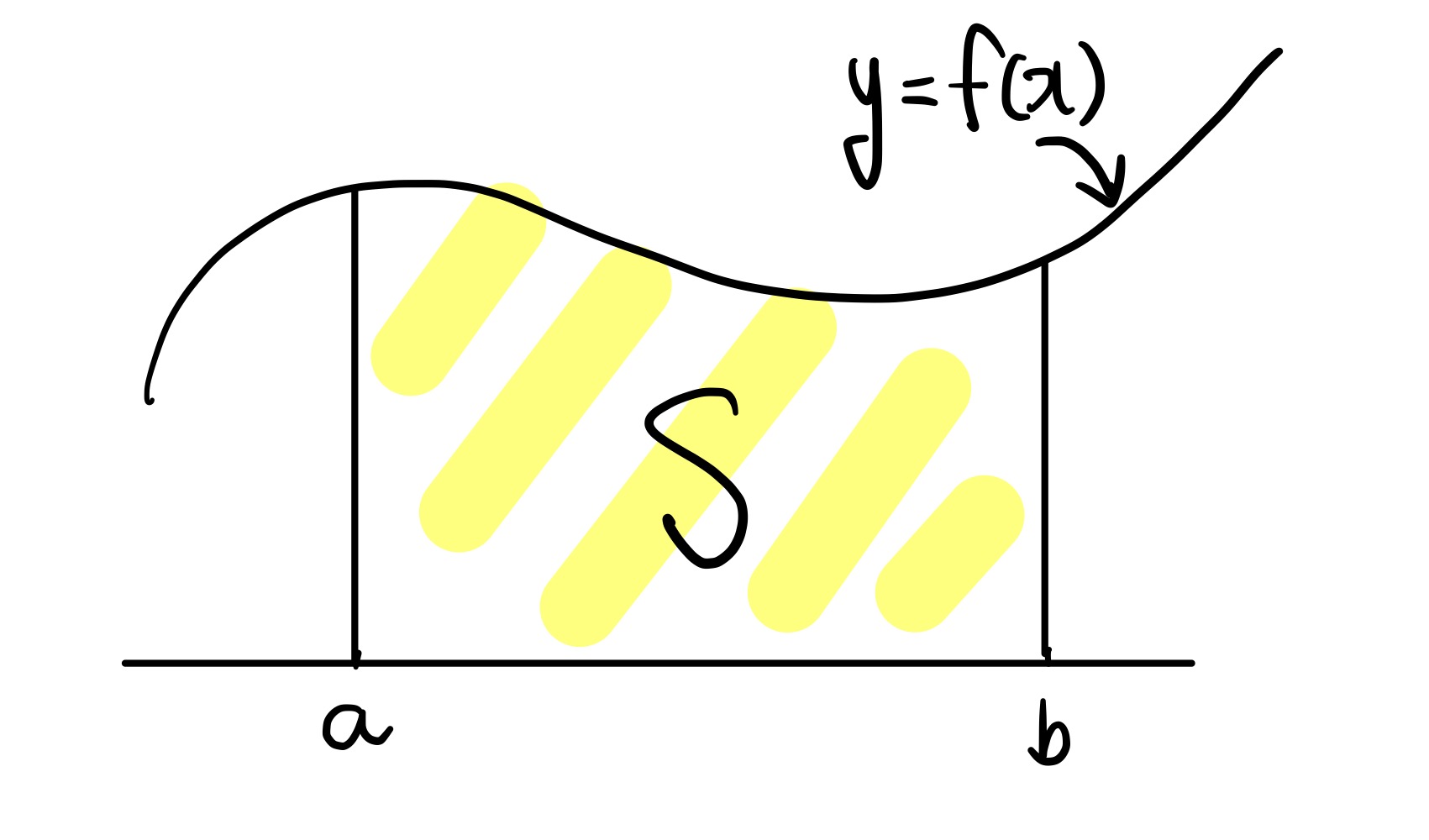
1. 함수 f가 구간 [a,b]에서 연속이고 f(x) ≥0이면,
함수 y=f(x)의 그래프와 x축 및
두 직선 x=a, x=b로 둘러싸인 도형의 넓이 S는

로 주어진다.
2. 회전체의 부피
이제 구간 [a,b]에서 f(x)≥0이라 하자.
이때, 곡선 y=f(x)와 x축 및 두 직선
x=a, x=b로 둘러싸인 도형을
x축 둘레로 1회전 시키면, 입체도형이 생긴다.
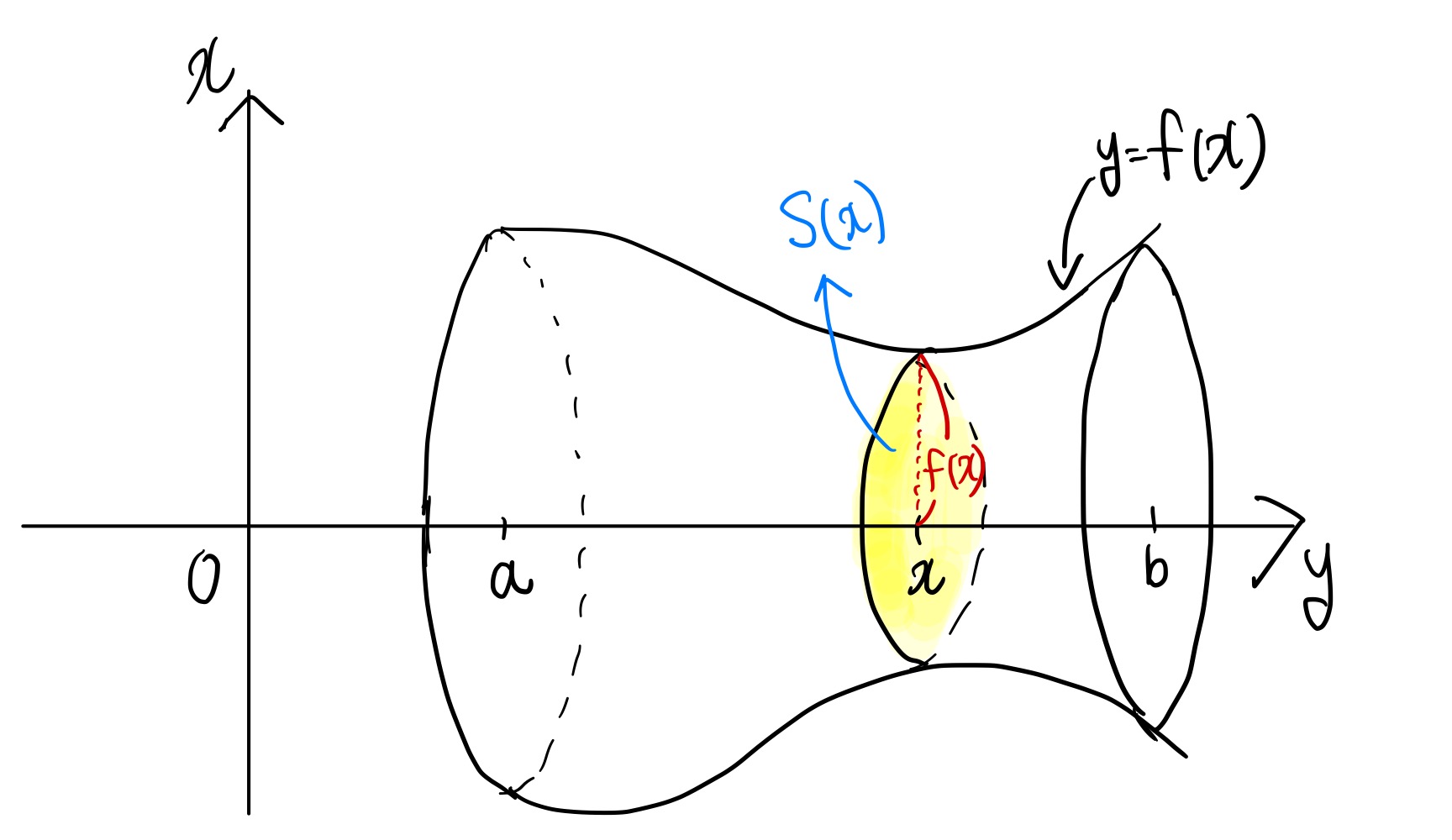
이 입체를 구간 [a,b]에서 곡선 y=f(x)를
x축을 기준으로 회전하여 생기는 회전체라고 한다.
이 회전체는 곡선 y=f(x)가 회전하여 생기는 곡면이고,
양쪽의 밑면은 각각 f(a), f(b)를
반지름으로 하는 원이다.
일반적으로 x축 위의 임의의 점 x(a≤x≤b)를 지나고,
x축에 수직인 평면으로 이 회전체를 자르면,
단면은 반지름이 f(x)인 원이 된다.
따라서, 회전체의 단면의 넓이를 S(x)라고 하면
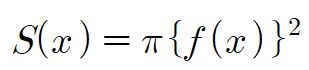
이다.
따라서, 구간 [a,b]에서 f(x) ≥0일 때,
y=f(x)를 이 구간에서 x축을 기준으로
1회전 시켜서 생긴 회전체의 부피 V는

로 주어진다.
반지름이 r인 구의 부피를 구해보자.
방법1. 회전체 적분 이용
반지름이 r인 구는, 반원
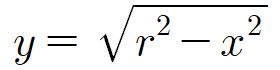
이 아래의 구간

에서 x축 둘레로 1회전하여 생기는
회전체로 생각할 수 있다.

따라서 그 부피 V는
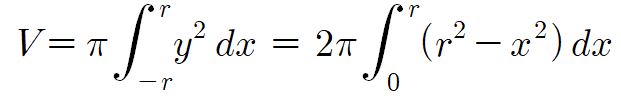

방법2. 구분구적분 이용
반지름이 r인 구의 부피는 반구의 부피의 2배이다.
따라서 구분구적법을 이용하여 반구의 부피를 구하고
그 값을 2배하면 구의 부피가 나온다.
반구의 높이 r을 일정한 간격으로 나눠서
밑면과 평행하게 절단하여
아래 그림과 같이 원기둥 조각으로 나눠보자.
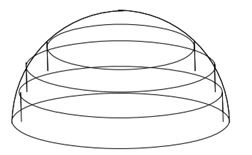
그러면, 반구의 부피는
무수히 많은 원기둥 부피의 합이다.
이때 생기는 원기둥들의 높이는 모두

이고,
k번째 원기둥의 밑면의 반지름을 R이라고 하면
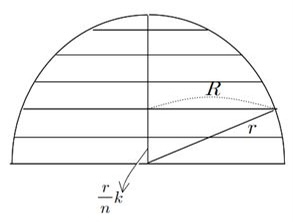
피타고라스의 정리에 의해
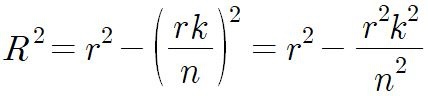
이므로
k번째 원기둥의 부피 V는
밑넓이와 높이를 곱한 아래의 값이 나온다.

이제 아래의 첫번째부터 n-1번째까지의
모든 원기둥들의 부피를 더해보자.

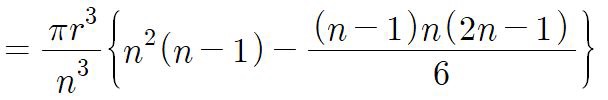
그리고 반구의 부피가 되려면
원기둥을 무한히 많이 잘라야 하므로

극한을 사용하자.

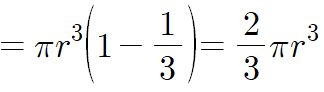
이 값에 2배를 하면 구의 부피
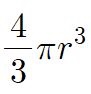
값이 나온다.
이제 구의 겉넓이를 구해보려 하는데….
이 방법을 이해하기 위해
한 차원 낮은 도형인 원의 입장에서 방법을
유추해 보겠다.
구에게 겉넓이란,
원에게는 원주의 길이일 것이다.
반지름이 r인 원의 둘레의 길이가 2πr임을 유도해 보자.
반지름이 r인 원의 둘레의 길이를 L(r)이라 하자.
아래 그림과 같이 반지름을 작은 수 h>0만큼
늘인 반지름이 (r+h)인 원을 생각해 보자.

큰 원과 작은 원의 넓이의 차는
그림의 띠 모양의 넓이다.
이 넓이는 작은 원의 둘레와 h를 두 변으로 하는
직사각형의 넓이보다는 클 것이고,
큰 원의 둘레와 h를 두 변으로 하는
직사각형의 넓이보다는 작다.

그런데 우리는 원의 넓이 공식을 알고 있기 때문에
이를 사용하면, 띠의 넓이는
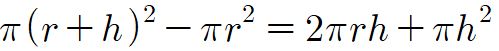
이다.
그러므로, 부등식

을 얻는다.
이 부등식의 각 변을 양수 h로 나누면,

가 된다.
여기서 h->0일 때의 극한을 생각하면,
부등식
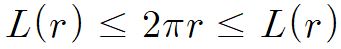
가 나온다.
따라서
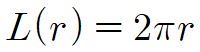
이다.
마찬가지 방법으로
구의 겉넓이를 구해보자.
반지름이 r인 구의 겉넓이를 S(r)이라고 하자.
작은 수 h>0에 대해
반지름이 (r+h)인 구를 생각하자.

이때, 큰 구와 작은 구 사이에 있는 부분인
테두리 공간의 부피는
S(r)h보다는 크고
S(r+h)h보다는 작다.
즉,

여기에서 테두리 공간의 부피는
반지름이 (r+h)인 구의 부피에서
반지름이 r인 구의 부피를 뺀 것이므로

이다.
여기서

이 식을 계산하면

이 되고,
따라서

이다.
이 부등식의 각 변을 양수 h로 나누면, 부등식
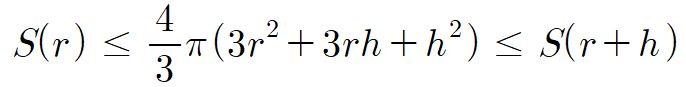
가 나온다.
여기서 h를 0에 가까이하면,
S(r+h)는 S(r)에 가까워지고,
부등식의 중앙의 항이

에 가까워진다.
그러므로

이고

이 나온다.
따라서
반지름의 길이가 r인 구의 겉넓이는

실험으로 끝나서
뭔가 찝찝함을 가지고 있던 학생들의
궁금증이 어느 정도 해소되었길 바라지만,
중학생이 이 글을 봤을 때
이해가 안 되는 것은 어쩌면 당연한 것일지도 모르겠다.
여러분이 고등학교 과정인
미적분, 극한을 배운다면
언젠가는 충분히 이해할 수 있을 테니
절~대 수학을 포기하지 않길 바란다.
'수학 이야기 > 중1수학' 카테고리의 다른 글
| 일차식의 덧셈, 뺄셈, 곱셈, 나눗셈, 응용 문제 (0) | 2024.08.05 |
|---|---|
| [입체도형]기둥, 뿔, 구의 부피 구하는 방법 (2) | 2023.01.09 |
| [입체도형]기둥, 뿔, 구의 겉넓이 구하는 방법 (0) | 2023.01.04 |
| [입체도형]정다면체(정다면체란?, 정다면체 그리는 방법) (0) | 2022.12.29 |
| [입체도형]다면체(각기둥, 각뿔, 각뿔대) (2) | 2022.12.28 |



