2015년도부터 체험수학에 관심을 갖기 시작했고
관련 연수와 수학체험전, MF 등을
다니면서 다양한 수학 관련 체험활동들을
경험해보고 학생들에게 가르치게 되었다.
어떤 연수인지는 기억나지 않지만
어디선가
아르키메데스의 다면체를 준정다면체라고 배웠고
그 사실에 의심을 하지 않고
학생들에게도 똑같이 가르쳤다.
그런데 2021년 참여하고 있는
수학교사 모임에서
아르키메데스의 다면체와
준정다면체는 다르다는 연수를 받고
나처럼 이 두 개념을 같다고 생각하는
학생, 선생님들을 위해
내용을 정리해본다.
아르키메데스의 다면체는
준정다면체가 아니다!!
우선 모든 수학적 개념을
정의를 통해 살펴보자.
정의의 출처는

그림의 출처는 '나'!
(힘든 과정이었다.)
정다면체(Platonic solid, 플라톤 다면체)란,

조건1. 모든 면이 합동인 정다각형으로 이루어져 있으며,
조건2. 각 꼭짓점에서 만나는 면의 개수가 같은 도형을 말한다.
아르키메데스의 다면체는
아래의 두 조건을 만족하는 다면체이다.
조건1. 두 종류 이상의 정다각형으로 이루어져 있으며,
조건2. 각 꼭짓점에 모인 면의 배치가 서로 같은 다면체이다.
(※각기둥과 엇각기둥을 제외한 다면체이다.)
아르키메데스의 다면체 정의를 알았으니
이제 어떻게 하면 아르키메데스의 다면체를
만들 수 있는지 살펴보자.
[방법 1] Truncate
모서리를 일부 남기고
꼭짓점을 자르는 방법이다.
이 방법으로는 5개의 아르키메데스 다면체가 생성된다.
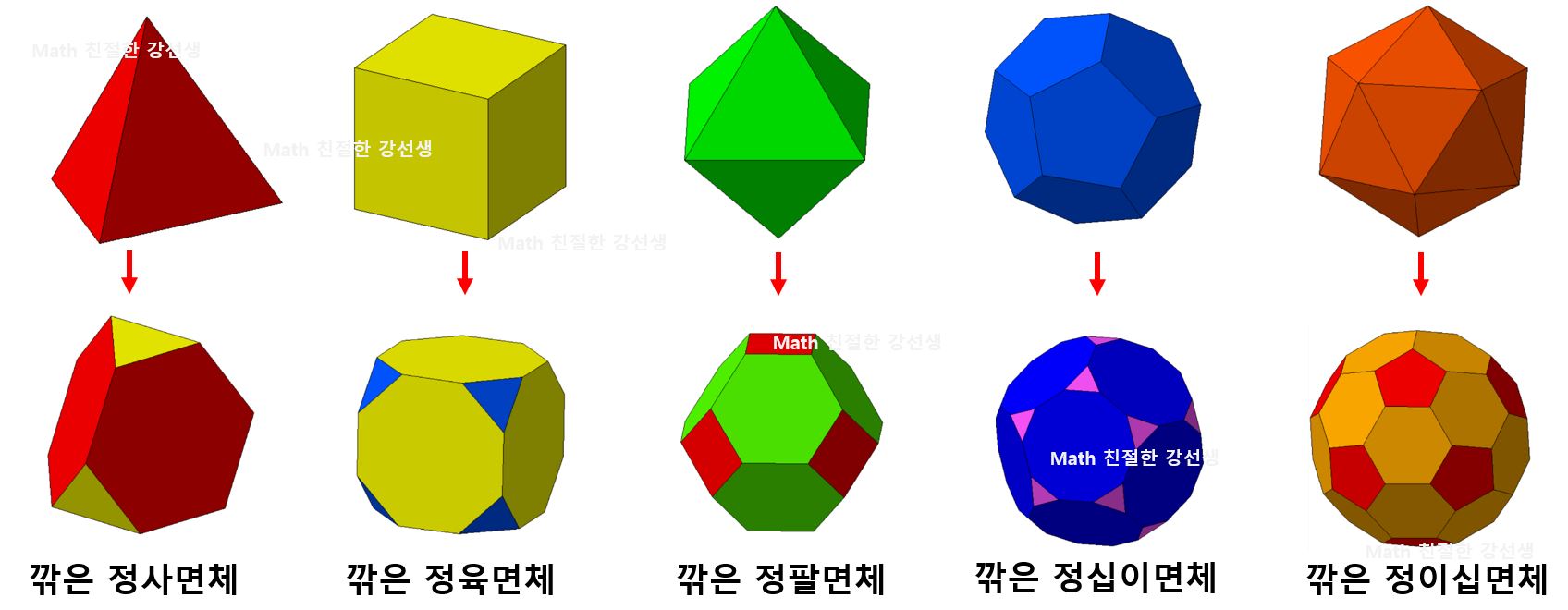
여기서!
깎은 정사면체, 깎은 정팔면체, 깎은 정이십면체는
잘린 면도 정다각형이어야 하므로
각각의 정다면체의
모서리를 꼭짓점으로부터 1/3 지점까지
잘라내야 한다.
즉 모서리를 1:1:1로 나눈 것이다.
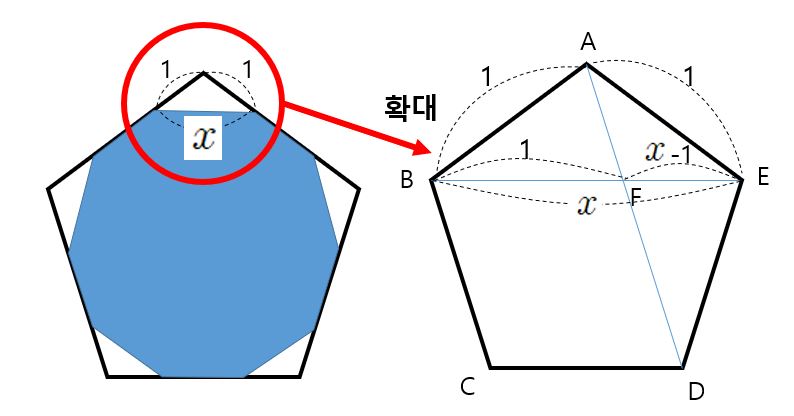
깎은 정육면체와 깎은 정십이면체는 다르다.
생각해보자.
잘려서 남겨진 면이 각각
정팔각형, 정십각형! 즉, 정다각형이어야 한다.
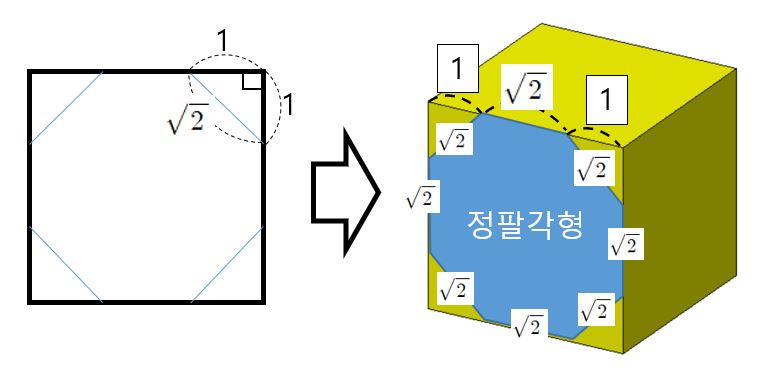
위의 그림에서 설명된 것처럼
깎은 정육면체는
정육면체의 각 모서리를
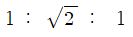
이 비율이 되게 잘라내어야 한다.
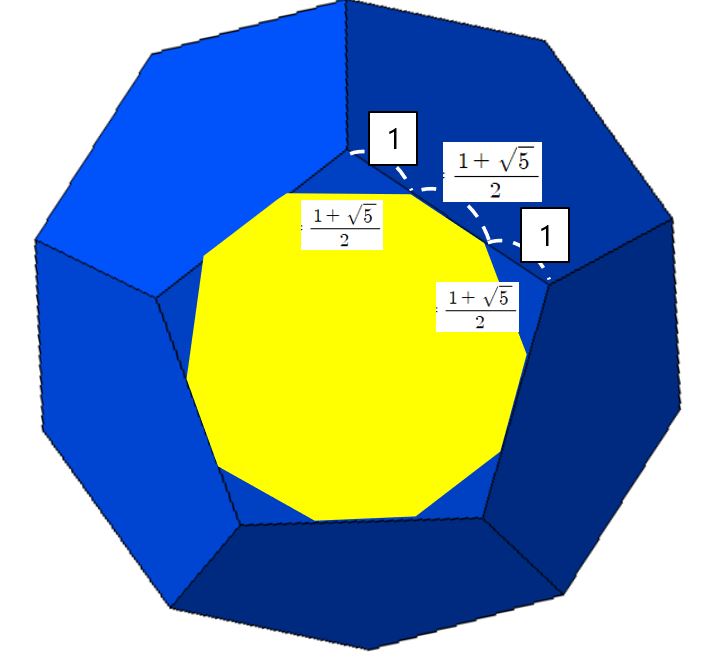
깎은 정십이면체는
정십이면체의 각 모서리를
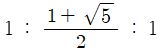
이 비율이 되도록 잘라내어야 한다.
이유는 아래와 같다.

[방법 2] Ambo
모서리를 남기지 않고 꼭짓점을 자르는 방법이다.
이 방법으로 2개의 아르키메데스 다면체가 생성된다.
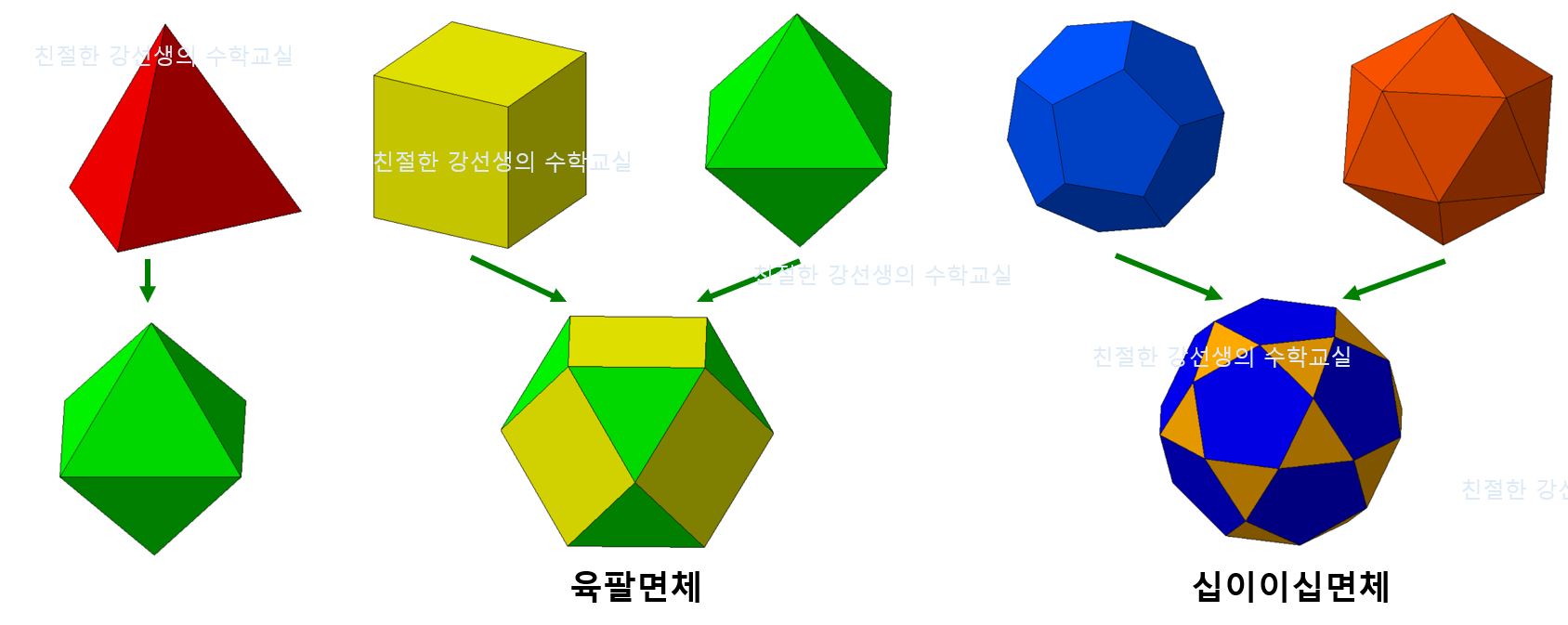
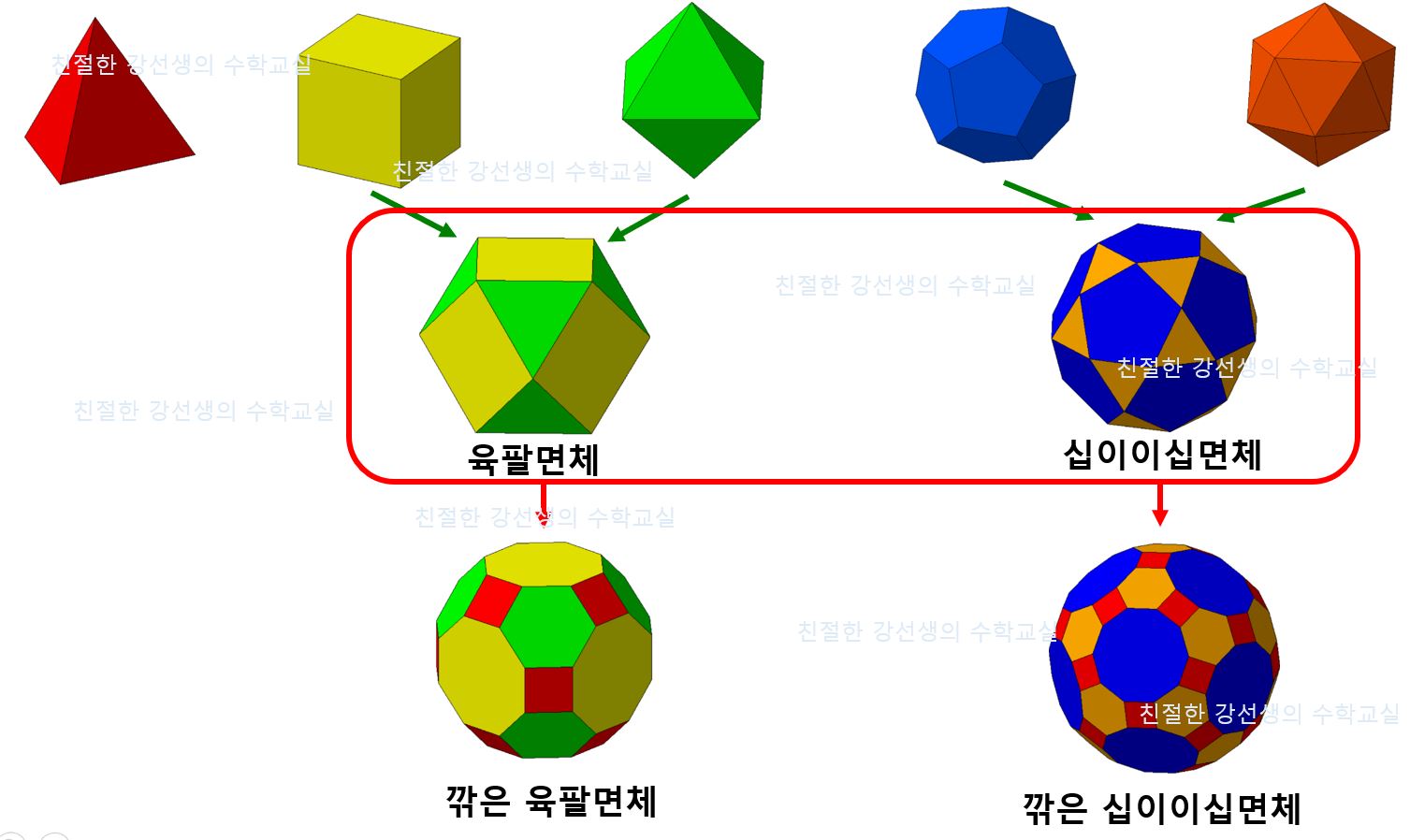
[방법 3] 육팔면체와 십이이십면체 Truncate
육팔면체와 십이이십면체를 대상으로
Truncate 방법을 적용하면
깎은 육팔면체, 깎은 십이이십면체,
이 두 개의 아르키메데스 다면체가 생성된다.
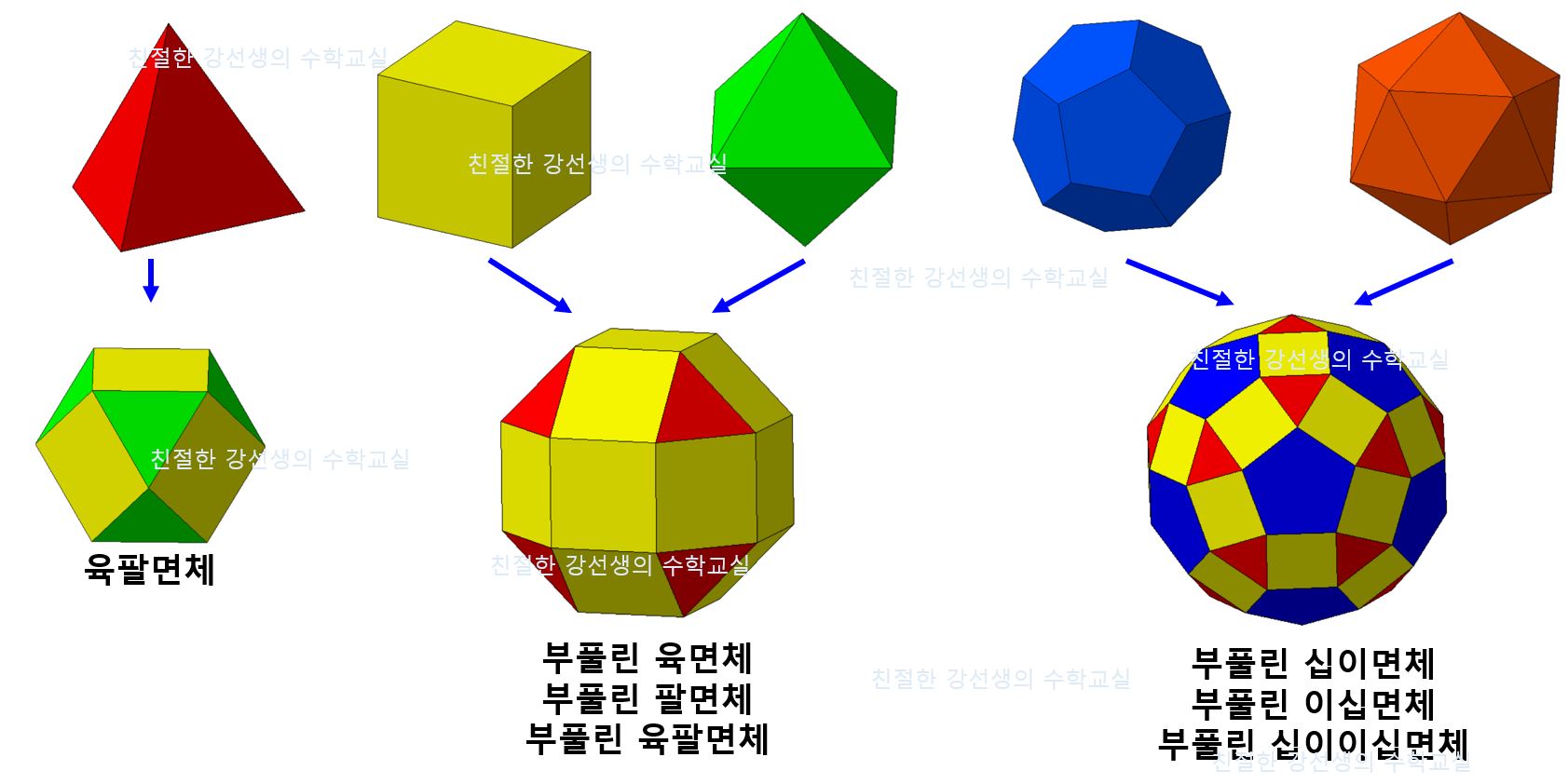
[방법 4] Expand
정다면체를 부풀려
모서리 사이를 정사각형으로 채우는 방법이다.
이 방법으로
부풀린 육팔면체와 부풀린 십이이십면체가 생성된다.
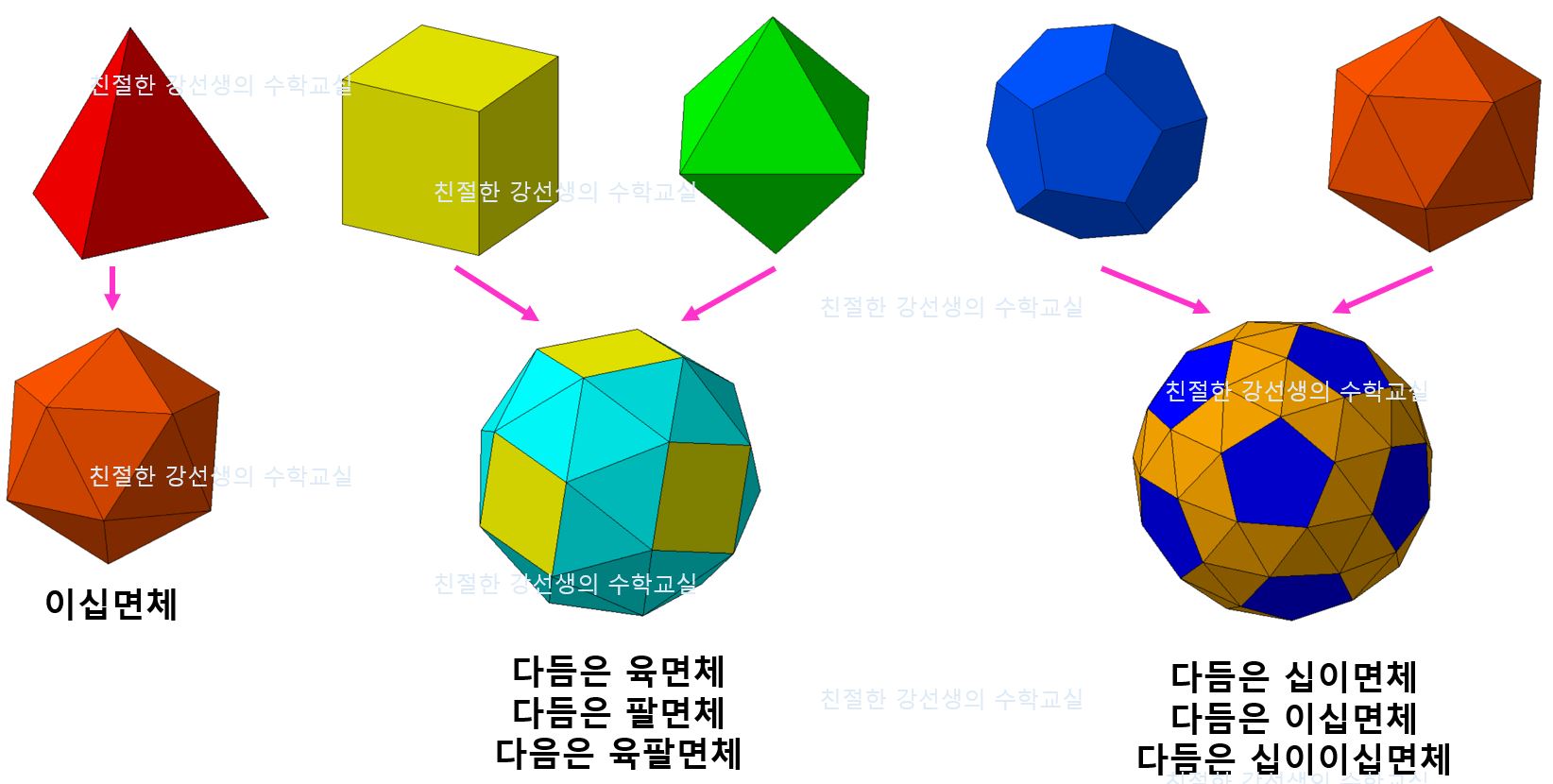
면을 따로 비틀어 이동하고,
모서리에 정삼각형 2개를 추가해
빈 부분을 채우는 방법이다.
이 방법으로
다듬은 육팔면체와 다듬은 십이이십면체가 등장한다.
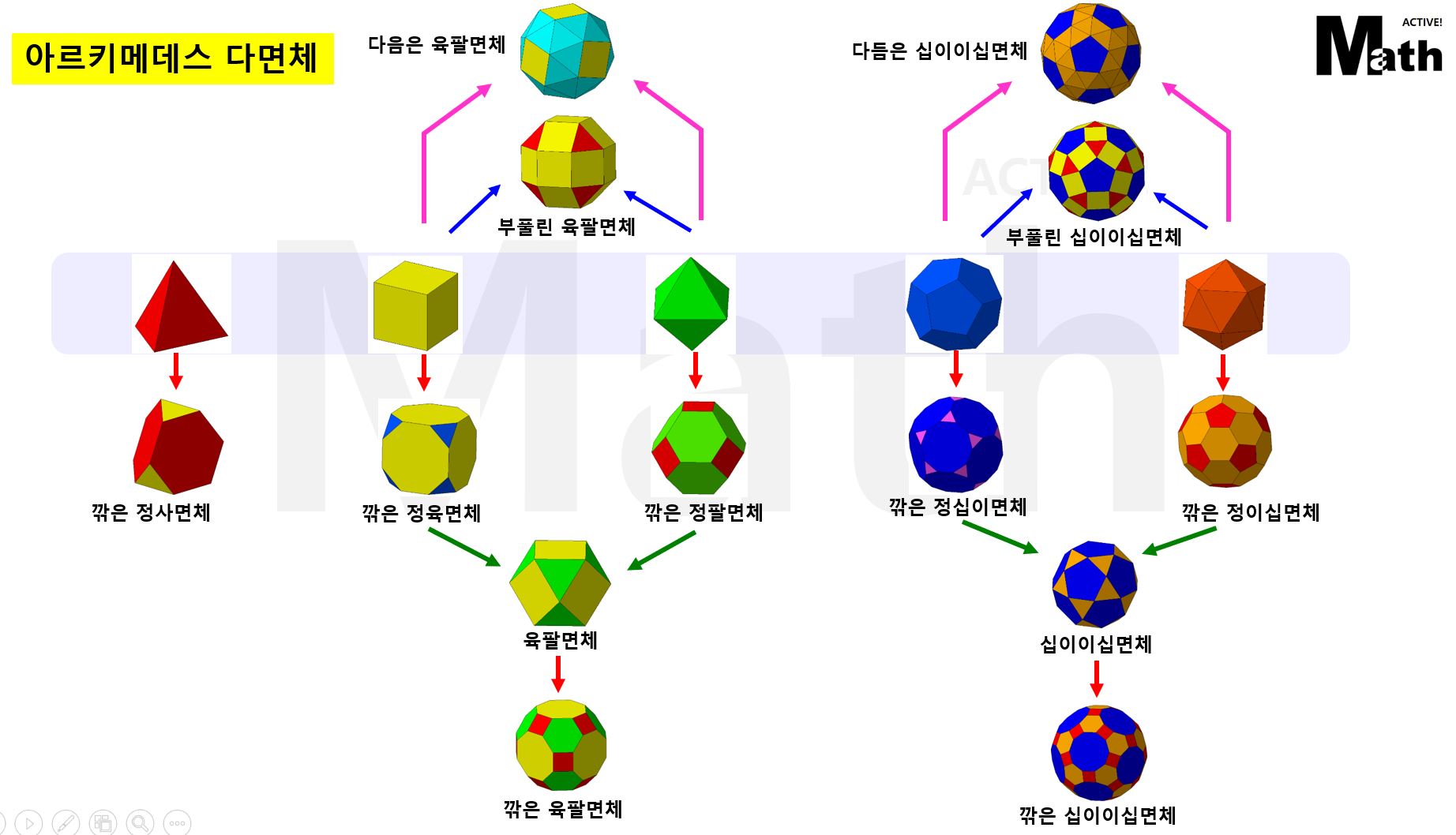
이렇게 해서 아르키메데스의 다면체는
총 13가지가 있다.
그렇다면 이제 준정다면체의 조건을 알아보자.
준정다면체는 아래의 두 조건을 만족하는 다면체이다.
조건1. 두 개의 정다각형을 사용하고
조건2. 각 모서리들이 서로 추이적(edge-trasitive) 관계인 다면체
(※ 반정다면체(semiregular polyhedron)와는 조금 다르다.)
★여기서 변추이(edge-transitive)란,
다면체에서 모든 모서리가 합동인 것이다.
단순히 모서리 길이와 이면각 뿐 아니라
모서리 주변 면의 배열까지 같아야 한다.
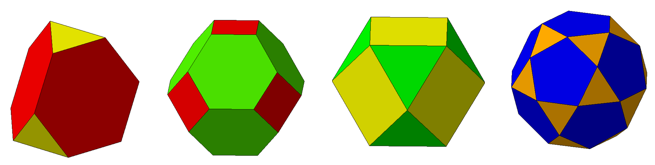
따라서 이를 만족하는 준정다면체는
아래와 같은 4가지 다면체이다.
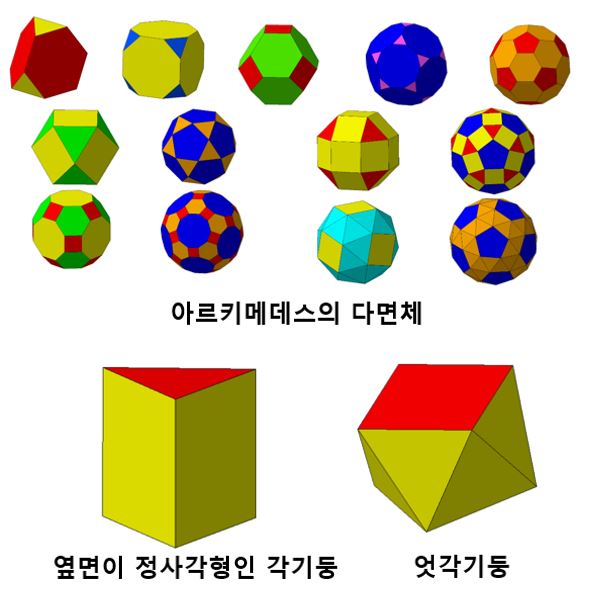
참고로 반정다면체에대해서 알아보면
조건1. 두 종류 이상의 정다각형으로 이루어져 있으며,
조건2. 각 꼭짓점에 모인 면의 배치가 서로 같은 다면체이다.
이를 만족하는 입체는
아르키메데스의 다면체와
옆면이 정사각형인 각기둥,엇각기둥이 있다.
수학적 개념은 정확한 정의를 검색해보고
관련 내용을 익히는 것이 중요하다.
'수학으로 놀자 > 수학체험' 카테고리의 다른 글
| 암호의 세계 (0) | 2023.03.20 |
|---|---|
| 재미있는 네모네모 로직 (0) | 2022.12.07 |
| 페르마의 밀실 영화 속 수학 논리 문제 해결하기2 (0) | 2022.10.06 |
| 페르마의 밀실 영화 속 수학 논리 문제 해결하기1 (1) | 2022.10.05 |



