중학교 수학을 대충 공부한 학생들을 위해 준비했다.
고등학교 가기 전에 읽고 가렴~~
중학교 수학을 영역별로 복습해 보자.
함수
목차부터 살펴보자.
[중2] 일차함수와 그래프
1. 함수의 뜻
2. 일차함수의 그래프
3. 일차함수의 그래프의 절편과 기울기
4. 일차함수의 그래프의 성질
5. 일차함수의 식 구하기
6. 일차함수와 일차방정식
7. 두 일차함수의 그래프와 연립일차방정식
[중3] 이차함수와 그래프

중2 함수 내용 정리
1. 함수: 두 변수 x, y에 대하여 x의 값이 변함에 따라 y의 값이 하나씩 정해지는 대응 관계가 있을 때, y를 x의 함수라고 한다.
* 변수 : x, y와 같이 변하는 여러 가지 값을 나타내는 문자
* 자연수 x의 5배인 자연수를 y라고 하자.
x의 값이 1,2,3,...으로 변함에 따라 y의 값은 5, 10, 15, ...와 같이 하나씩 정해지는 대응 관계가 있으므로 y는 x의 함수이다.
* 자연수 x보다 작은 자연수를 y라고 하자.
x의 값이 3이면 y의 값은 1,2이다. x의 값 하나에 y의 값이 하나로 정해지지 않으므로 y는 x의 함수가 아니다.
2. 일차함수 : 함수 y=f(x)에서 y가 x에 대한 일차식 y=ax+b(단, a, b는 상수, a≠0)로 나타날 때, 이 함수를 x에 대한 일차함수라고 한다.
* y=x+1, y=5x-4 : 일차함수
x+1=0, 5x-4=0 :일차방정식
x+1>0, 5x-4<0 :일차부등식
x+1, 5x-4 :일차식
3. 일차함수의 그래프의 그리기 : 방법1. 평행이동
y=2x와 y=2x+3 그래프 사이의 관계를 살펴보자.

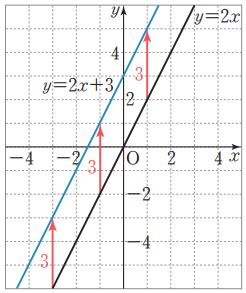
* 평행이동 : 한 도형을 일정한 방향으로 일정한 거리만큼 옮기는 것
* 일차함수 y=ax+b의 그래프는 일차함수 y=ax의 그래프를 y축의 방향으로 b만큼 평행이동한 직선이다.
* y=ax그래프는 그리기 쉬우니, y=ax그래프를 먼저 그리고 상수 b값만큼 세로 방향으로 움직이기!!
여기서 b가 음수이면 아래로 b만큼 평행이동 하고, b가 양수이면 위로 b만큼 평행이동!
4. 일차함수의 그래프 그리기 : 방법2. x절편, y절편
* x절편 : 일차함수의 그래프가 x축과 만나는 점의 x좌표
-> 그래프가 x축과 만난다는 것은 높이가 0일 때를 말하므로 함수식에서 y=0일 때의 x의 값을 구하면 된다.
* y절편 : 일차함수의 그래프가 y축과 만나는 점의 y좌표
-> 그래프가 y축과 만난다는 것은 x축 좌우로 움직임이 없다는 것이므로 x=0일 때의 y의 값을 구하면 된다.
* y=-2x+2로 살펴보자. y=0 대입하면, 0=-2x+2, 방정식을 풀면 x=1이다. x=0을 대입하면 y=2이다.
즉, y=-2x+2 그래프는 x축과 1에서 만나고, y축과는 2에서 만나기 때문에 그래프는 아래와 같다.
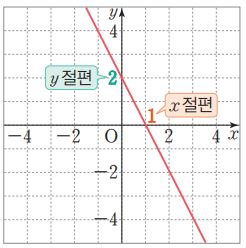
* y=ax+b의 그래프의 x절편은 -b/a, y절편은 b이다.
5. 일차함수의 그래프 그리기 : 방법3. 기울기와 y절편
* 기울기 : y=ax+b의 그래프는 직선이기 때문에 x값의 증가량에 대한 y의 값의 증가량의 비율(기울어진 정도)은 항상 일정하며, 그 비율은 x의 계수 a와 같다.
이 증가량의 비율 a를 일차함수 y=ax+b의 그래프의 기울기라고 한다.
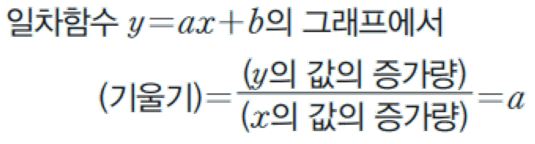
* 서로 다른 두 점 (a,b), (c,d)를 지나는 일차함수의 그래프의 기울기는 (d-b)/(c-a) 또는 (b-d)/(a-c)로 구할 수 있다.
* y절편을 이용하여 y축과 만나는 한 점을 좌표평면 위에 찍고! 기울기를 이용하여 그래프 위의 다른 한 점을 찾는다.
그리고 그 두 점을 직선으로 연결하면 일차함수 그래프를 빠르게 그릴 수 있다.
* y=4x-3 그래프 그리기 : y절편 -3이므로 (0,-3)에 점찍고, 기울기가 4이므로 x값 1증가할 때 y의 값은 4만큼 증가하므로
(0+1, -3+4)=(1,1)이 그래프 위의 다른 한 점이 된다. 이 두 점을 이으면 일차함수 그래프 완성!
6. 일차함수 y=ax+b의 그래프의 성질
* a>0일 때, 그래프는 오른쪽 위로 향하는 직선이다. 즉 x의 값이 증가할 때, y의 값도 증가한다.
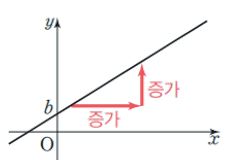
* a<0일 때, 그래프는 오른쪽 아래로 향하는 직선이다. 즉, x의 값이 증가할 때, y의 값은 감소한다.
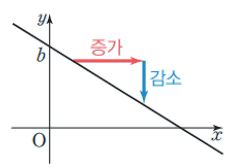
* 기울기가 같은 두 일차함수의 그래프는 서로 평행(y절편이 다를 때)하거나 일치(y절편도 같을 때)한다.
* 서로 평행한 두 일차함수의 그래프의 기울기는 서로 같다.
7. 기울기(3)와 한 점(-2,1)이 주어진 일차함수의 식 구하기
*순서1. 기울기가 3인 일차함수의 식을 y=3x+b로 나타내기
*순서2. 한 점의 좌표를 이용하여 y절편 b값 구하기
지나는 한 점이 (-2,1)이므로 x=-2를 y=1을 대입해 보자. 1=3×(-2)+b, b=1+6=7
*순서3. 일차함수의 식 구하기 : y=3x+7
8. 두 점(3,-2),(1,4)이 주어진 일차함수의 식 구하기
*순서1. 두 점의 좌표를 이용하여 기울기 a의 값 구하기
기울기 a={4-(-2)}/(1-3)=6/-2=-3
*순서2. 일차함수의 식을 y=ax+b꼴로 나타내기 : y=-3x+b
*순서3. 한 점의 좌표(내 맘대로)를 이용하여 y절편의 b값 구하기
(1,4) 너로 정했다! x=1, y=4 대입하면 4=-3+b, b=7
*순서 4. 일차함수의 식 구하기 y=-3x+7
9. 일차방정식 x=p, y=q의 그래프
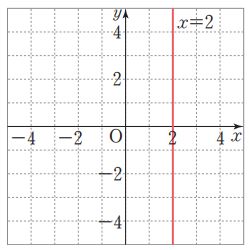
* x=p(단, p≠0)의 그래프는 점 (p,0)을 지나고 y축에 평행한 직선이다.
9번에서 일차함수라고 하지 않고 일차방정식의 그래프라고 한 것에 주목하자.
x=p는 x의 값 하나에 무수히 많은 y값이 대응하므로 함수가 아니다. 즉, 일차함수도 아니다.
하지만, 직선이므로 직선의 방정식 ax+by+c=0꼴로 표현할 수 있다. b=0인 경우가 되겠다.
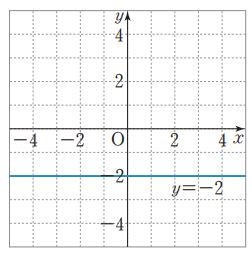
* y=q(단, q≠0)의 그래프는 점 (0,q)를 지나고 x축에 평행한 직선이다.
y= q는 x의 값이 변함에 따라 y의 값은 항상 2로 정해지므로 함수는 맞다.
하지만 y=ax+b에서 a=0이므로 일차함수는 아니다.
이런 함수를 상수함수라고 부른다.
10. 일차함수와 일차방정식의 관계
* 미지수가 2개인 일차방정식 ax+by+c=0(단, a≠0, b≠0)을 변신시켜 보자!

즉, 일차방정식 ax+by+c=0(a≠0, b≠0)을 만족하는 해의 순서쌍 (x, y)를 좌표평면 위에 나타내면,
그것은 일차함수 y=(-a/b)x-c/b의 그래프가 된다.
따라서 일차방정식 ax+by+c=0 (a≠0, b≠0)의 그래프는 결국!! 일차함수 y=(-a/b)x-c/b의 그래프와 같다.
참고로 고등학교에 가면 직선의 방정식 이라는 말이 등장하는데
일차방정식 ax+by+c=0이 나타내는 도형을 말한다.
즉, 직선의 방정식이란 일차함수(기울어져 있는 직선), 상수함수(가로 직선), x=p(세로직선)꼴과 같이
모든 형태의 직선을 수학적으로 표현하는!! 일차함수보다 더 폭넓은 개념으로 이해하면 되겠다.
11. 연립방정식의 해와 그래프
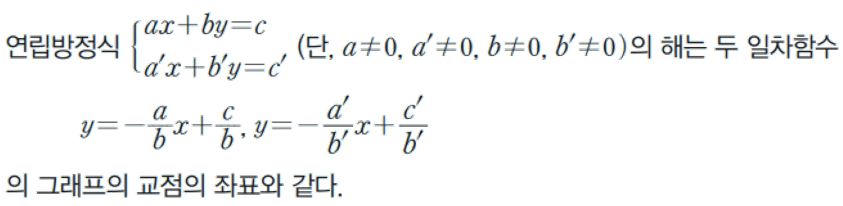
* 연립방정식에서 각 방정식의 그래프인 두 직선이 한 점에서 만나면 연립방정식의 해는 그 교점의 좌표 하나뿐이다.
* 연립방정식에서 각 방정식의 그래프가 평행하면 연립방정식의 해는 없다.
* 연립방정식에서 각 방정식의 그래프가 일치하면 연립방정식의 해는 무수히 많다.