IQ 148을 위한 추리 전쟁
CIA 범죄 퍼즐

이 책의 저자인 존 길라드(John Gillard)는
스파이와 추리의 세계에 흥미를 느끼고,
CIA의 첩보 기술을
퍼즐과 접목하는 방법을 연구한 끝에
세계적인 퍼즐 전문가인
개러스 무어의 자문을 거쳐
《CIA 범죄 퍼즐》을 집필했다.
CIA는 요원이 되기 위한 조건으로
사고의 유연성, 풍부한 지식,
명령체계의 존중 등을 요구한다.
CIA 대변인으로 근무한 첼시 로빈슨은
'다양한 분야의 지식과 기술'을
가장 중요한 덕목으로 제시했다.
이 책에 제시된 문제들은
총 5개 영역에 걸쳐
비밀요원에게 필요한
다방면의 역량을 시험한다.
퍼즐을 풀기 위해서는
논리적 사고력과 추리력은 물론
세계지리와 역사에 해박한 지식과
판단력, 공간지각력, 각종 첩보 기술을 비롯해
다양한 사고능력이 요구된다.
많은 문제들이 있지만
수학 시간에 학생들과
같이 풀어볼 만한 문제들을
소개해보고자 한다.
1. 금고 열기
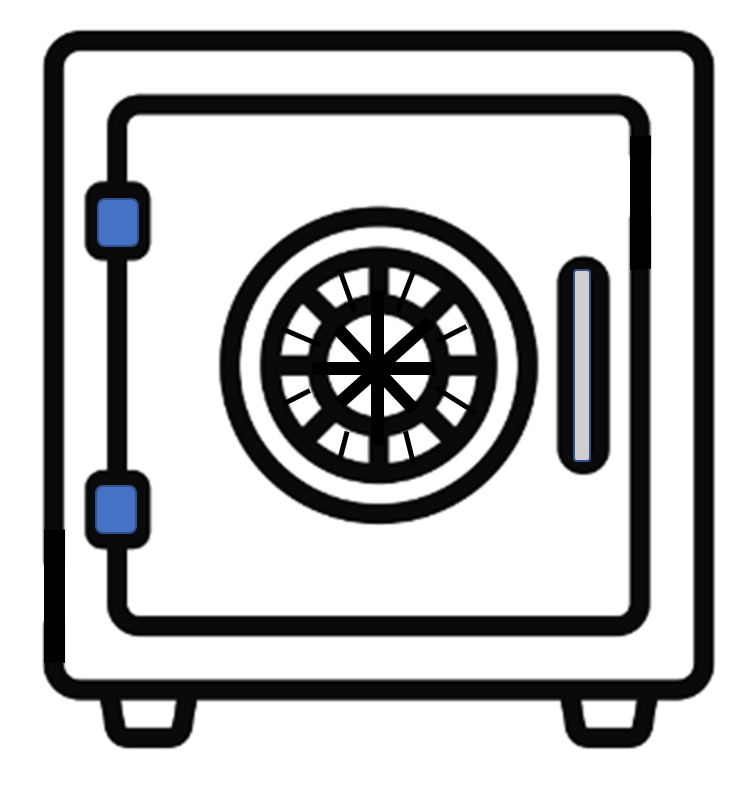
Q. 당신의 첫 번째 임무는 상대 비밀 요원의 근거지에 침입해 그가 갖고 있는 기밀문서를 빼돌리는 것이다.
처음부터 너무 어려운 임무를 받았다고 불평할지도 모르겠지만, 정보기관의 요원에게 쉬운 임무란 없다.
금고 다이얼의 바깥쪽 원에 있는 숫자들은 세 숫자를 제외하고 일정한 규칙에 따라 배치되어 있다.
규칙에 맞지 않는 세 숫자를 찾아 크기순으로 다이얼 아래 빈칸을 채우면 금고가 열린다.
빈칸에 들어갈 숫자 세 개는 무엇일까?
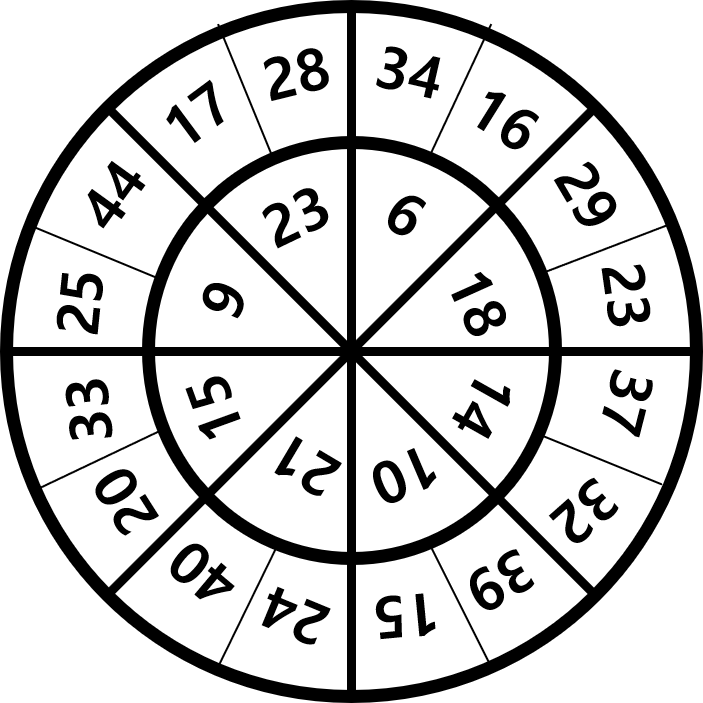

풀이)
문제 속에는 항상 힌트가 있다.
문제에서 금고 다이얼의 바깥쪽 원에 있는 숫자들은
세 숫자를 제외하고 일정한 규칙에 따라
배치되어 있다고 했다.
그렇다면 이 문제를 풀 때
바깥쪽 원에 있는 숫자와
안쪽 원에 있는 숫자의 관계를
파악해야 할 것이다.
부채꼴에서 바깥쪽의 두 수를
더하거나 곱하거나
다양하게 조합해서 계산해보았으나
안쪽에 있는 수와의 연관성을
찾지 못했다.
반대 방법으로 생각해보았다.
안쪽에 있는 수를 가지고
바깥쪽에 있는 수들을 만들 수 있는지
생각해보았다.
안쪽의 수 : 6, 9, 10, 14, 15, 18, 21, 23
34=
16=6+10
29=15+14
23=14+9
37=23+14
32=14+18
39=18+21
15=6+9
24=10+14
40=
20=6+14
33=15+18
25=10+15
17=
28=10+18
바깥쪽 숫자들 중
17, 34, 40을 제외하고는
안쪽에 있는 8개의 숫자의 합으로
나타낼 수 있다.
따라서 금고의 비밀번호는
173440이다!!!
2. 성냥개비로 할 수 있는 일
당신은 다른 요원과 함께 동유럽의 은신처에 숨어 있다.
은신처는 매우 기본적인 것만 갖춰져 있다.
테이블 하나, 의자 두 개, 침대 두 개, 약간의 기본 식량, 그리고 성냥 한 갑이 있다.
은신처에서 안전한 출국을 도와줄 본부의 연락을 기다리고 있지만,
소식이 오려면 짧게는 몇 시간, 길게는 며칠까지 걸릴 것이다.
동료가 말했다.
"연락이 오려면 시간이 많이 남았어.
심심풀이로 내가 내는 퀴즈를 푸는 건 어때?"
그는 성냥갑을 들고 오도니 성냥들을 늘어놓았다.
성냥개비 퍼즐을 해결해보자.
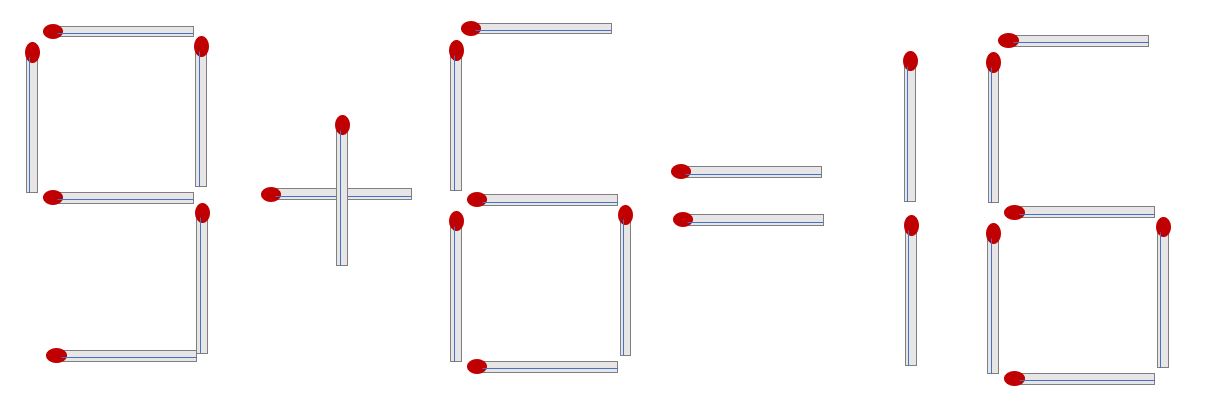
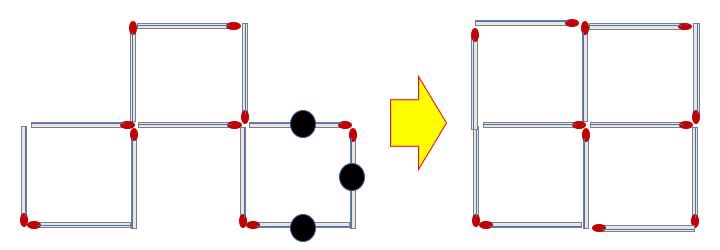
Q1) 성냥개비 3개를 움직여 정사각형 4개를 만들어라.
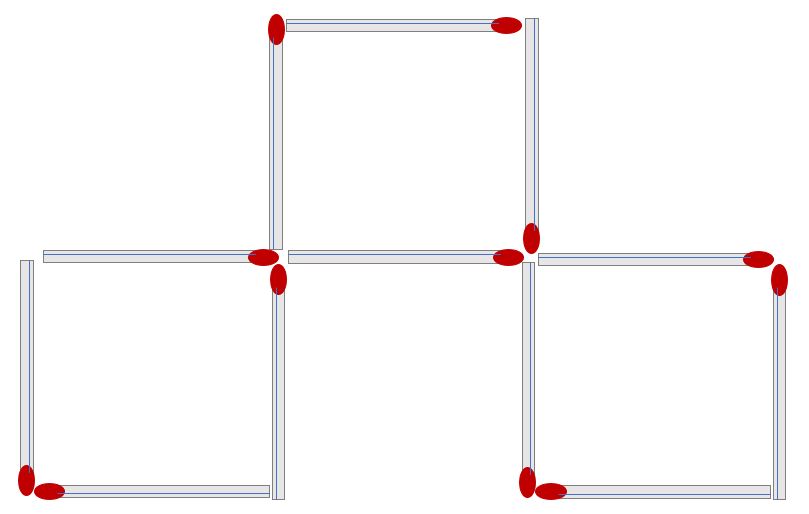
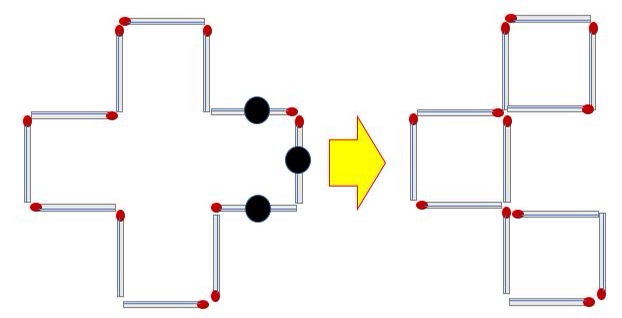
Q2) 성냥개비 3개를 움직여 정사각형 3개를 만들어라.
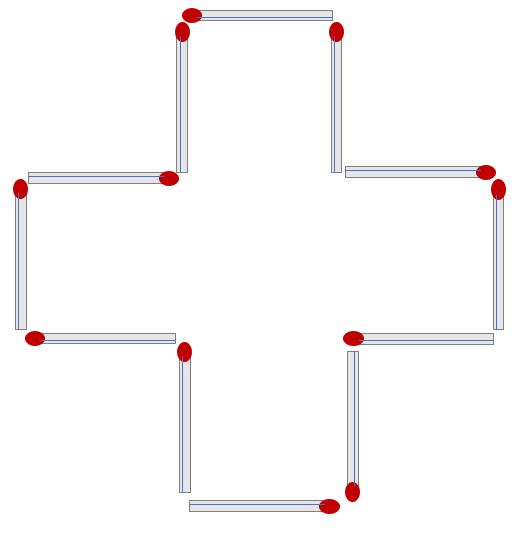
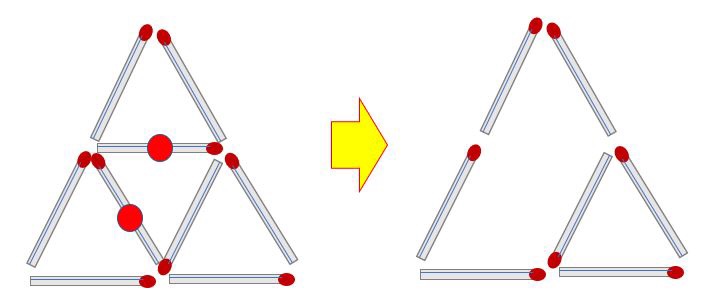
Q3) 성냥개비 2개를 없애 삼각형 2개를 만들어라.
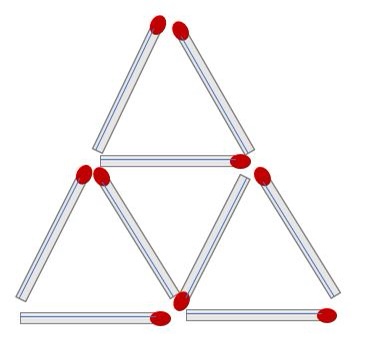
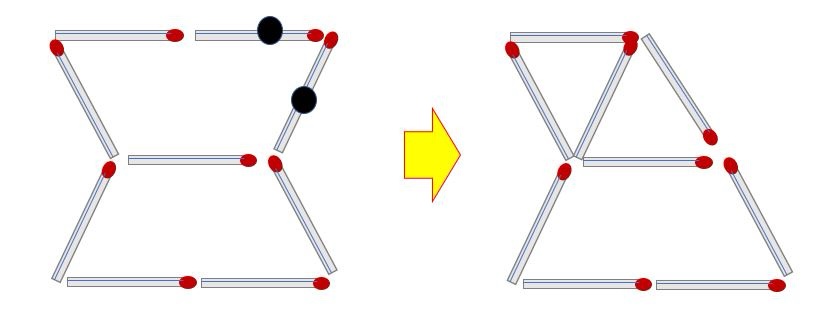
Q4) 성냥개비 3개를 움직여 삼각형 3개를 만들어라.
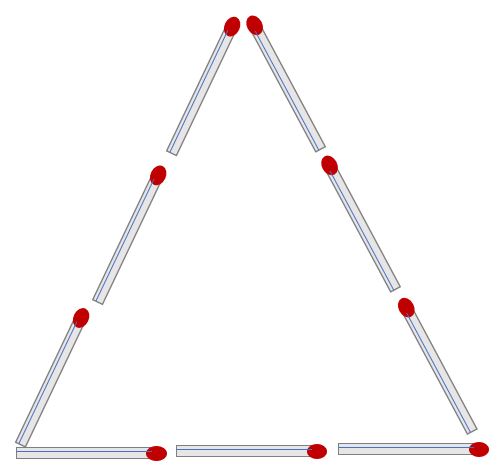
Q5) 성냥개비 2개를 움직여 삼각형 3개를 만들어라.
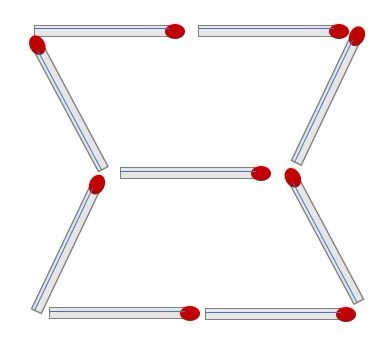
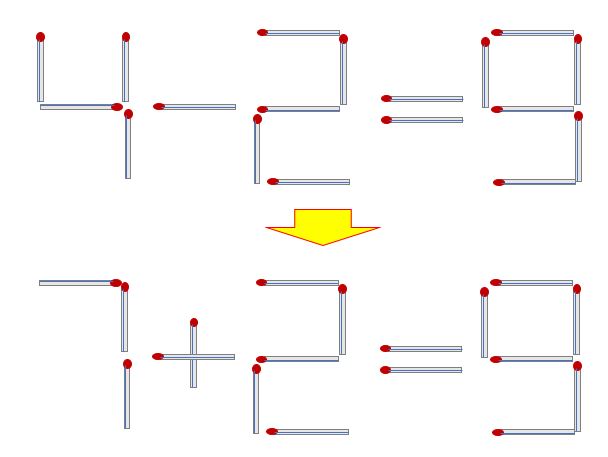
Q6) 성냥개비 2개를 움직여 다음 계산이 성립하도록 만들어라.
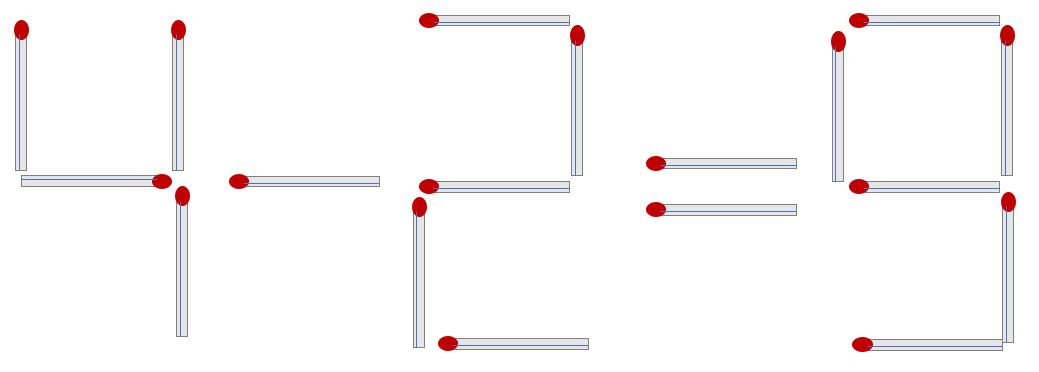
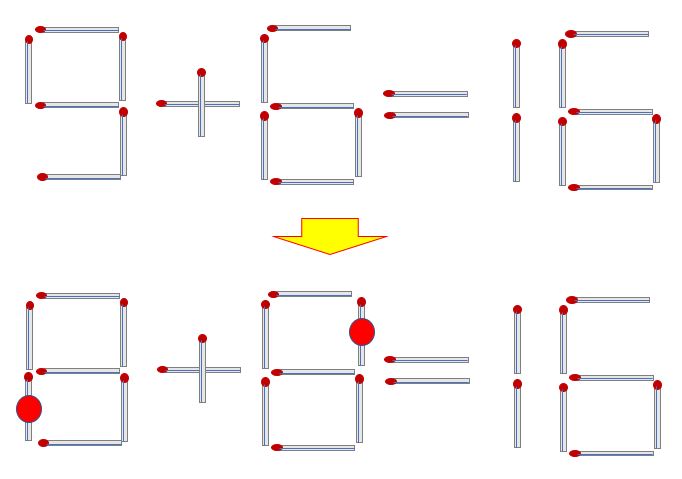
Q7) 성냥개비 2개를 더해 다음 계산이 성립하도록 만들어라.
(정답 1)
(정답 2)
(정답 3)
(정답 4)
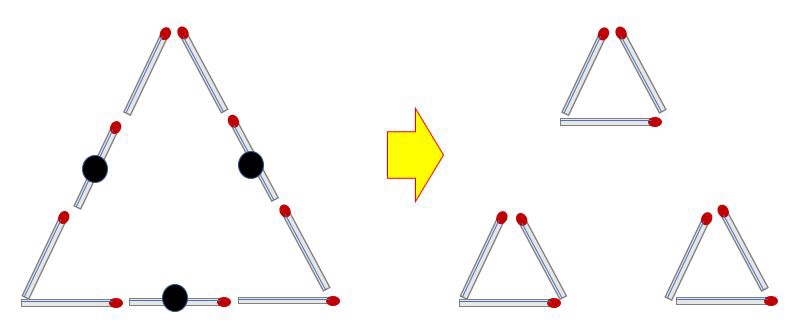
(정답 5)
(정답 6)
(정답 7)
이 두 문제 이외에도
최단경로를 찾는 문제,
아홉 개의 점을 잇는 문제,
모스부호를 이용하여 메시지를 해독하는 문제 등
다양하고 재미있는 문제가 많이 수록되어 있으니
논리 퍼즐에 관심 있다면 추천한다.
하지만 수학적인 논리를 이용하는 문제보다
세계지리와 역사 관련 문제들이 훨씬 많다.
따라서 다양한 분야의 지식을 활용하여
문제를 해결하는데 관심 있는 분들께 추천한다.