[입체도형]기둥, 뿔, 구의 부피 구하는 방법

부피란, 

공간에서 한 물체가 차지하는

양을 뜻한다.

 

 

즉, 수학에서는

입체도형이 공간에서 차지하는

크기를 말하며,

부피의 단위에는

㎤(세제곱센티미터),

㎥(세제곱미터)가 있다.

 

 

 

오늘은 기둥, 뿔, 구의

부피를 구하는 방법을 알아보자.

 

[기둥의 부피]

기둥의 부피를 구하는 방법은

아~~주 간단하다.

 

각기둥이든지 원기둥이든지

밑면이 높이만큼 쌓여있기 때문에

 

기둥의 부피는

(밑넓이)×(높이)

 

각기둥의 부피를 구해보자.

밑넓이=5×8×1/2=20㎠

높이=6cm

부피= 20×6=120㎤

 

 

이번에는 원기둥의 부피도 구해보자.

밑넓이=4×4×π=16π㎠

높이=10cm

부피 = 16π ×10=160π ㎤

 

 

 

 

[뿔의 부피]

뿔의 부피는 기둥의 부피의 

이라는 사실만 안다면

뿔의 부피를 구하는 것도 어렵지 않다.

 

중1 수준에서는 이를

실험을 통해 직관적으로

학생들에게 이해시킨다.

 

수업시간에는

실제로 실험을 하기보다는

잘 만들어진 

ebs math영상을 보여준다.

 

https://www.ebsmath.co.kr/url/go/108469

밑넓이와 높이가 같은

원기둥과 원뿔이 있다.

 

원뿔 용기에 과자를 채워

원기둥 용기에 3번 담으면

원기둥 용기에

과자가 가득 찬다.

 

 

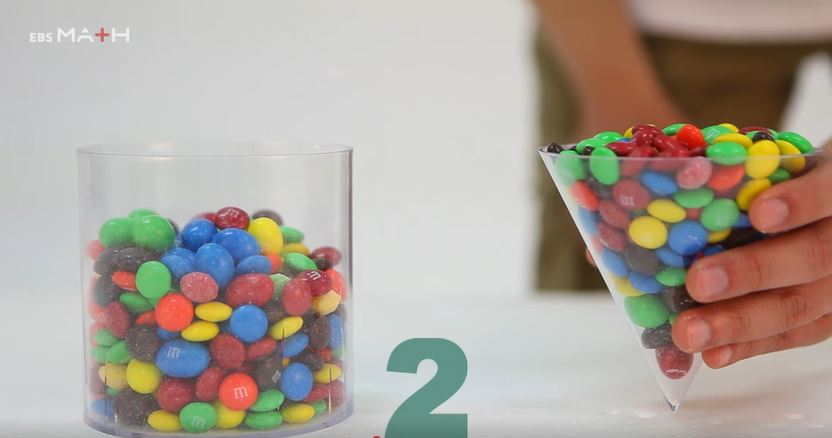
즉, 뿔의 부피는

각뿔이든 원뿔이든

 

 

직접 구해보자.

밑넓이=8×7×1/2=28 ㎠

높이 = 12cm

부피 = 1/3×28×12=112㎤

 

 

 

이번에는 원뿔의 부피를 구해보자.

밑넓이=25π ㎠

높이 =9cm

부피=1/3×25π×9=75π ㎠

 

 

---

여기서 잠깐!!

고등학교 과정이지만,

적분을 이용한 방법이 궁금한 

학생들이 있을 수도 있으니...

 

 

밑넓이가 S, 높이가 h인 각 뿔의 부피를 구해보자.

 

각뿔의 꼭짓점을 O라 하고,

O를 지나 밑면에 수직인 직선이

x축이 되도록 한다.

밑면(밑면을 포함하는 평면)과

x축의 교점을 H라고 하면

각뿔의 높이가 h라고 했으니

H의 좌표는 h가 된다.

 

x축 위의 점 x(0≤x≤h)를 지나고

x축에 수직인 평면에 의해

잘린 각뿔의 단면의 넓이를 S(x)라고 하면,

 

S(x)와 S를 밑면으로 하는

두 각뿔은 닮음비가 x:h인 

닮은 입체도형이다.

 

따라서 밑면의 넓이의 비는

닮음비의 제곱이 된다.

 

즉,

이다.

 

그러므로 각뿔의 부피 V는

가 된다.

 

---

 

 

[구의 부피]

마지막으로 구의 부피를 구해보자.

중1 수준에서 이해 가능한 방법으로

최대한 수학적으로!

설명해 보겠다.

 

 

 

자!

반지름의 길이가 r인 구의 표면을

가로, 세로선으로 쪼갠다.

아~주 많이

 

그러면 구의 표면이

격자모양으로 쪼개어지는데

이 각각의 조각을 밑면으로 하고

꼭짓점을 구의 중심으로 하는

각뿔을 만들어보자.

 

구의 부피는 유한하므로

쪼개진 조각들도 유한할 것이다.

총 n개로 쪼개졌다고 하자.

 

조각들의 밑넓이를 각각

이라고 하면, 

n개의 각뿔의 높이는 모두 

구의 반지름 r이다.

 

 

따라서, 구의 부피

=n개의 각뿔의 부피의 합이므로

이 되고, 여기서 밑넓이들의 합은

결국 구의 겉넓이가 되므로

이다.

 

 

이를 대입하면, 결국 구의 부피는

이 나온다.

 

 

구의 부피를 적분을 이용하여 구해보고 싶다면

이 전에 올린 글을 참고할 것!