[입체도형]정다면체(정다면체란?, 정다면체 그리는 방법)
'정'이 붙은 다면체
정다면체를 학습하기 전에
'정'이 붙은 다각형인
정다각형부터 살펴보자.
정다각형이란,
1. 변의 길이가 모두 같고
2. 각의 크기가 모두 같은 다각형이다.

정다각형의 구조적 특징은
원에 내접한다는 것!
정다면체란,
1. 각 면이 모두 합동인 정다각형이고,
2. 각 꼭짓점에 모인 면의 개수가
모두 같은 다면체이다.
1번 조건은 정다각형에서
변의 길이가 같아야 한다는
조건이 확장된 것이고
2번 조건은 정다각형에서
각의 크기가 같다는 조건과
연관되어 있다.
입체도형에서 각이라 하면,
입체의 꼭짓점을 중심으로
꼭짓점에 모인 면들이 이루는
구부러진 정도로 이해해야 한다.
그 구부러진 정도가 같아지려면
당연히
각 꼭짓점에 모인 면의 개수가
같아야 할 수밖에 없다.

위의 다면체를 정다면체라고 할 수 있을까?
NO!!
빨간색 꼭짓점은
정삼각형이 3개 모여있기 때문에
정삼각형이 4개 모여있는
노란색 꼭짓점보다
면들 서로 더 모여있다.
즉, 2번 조건을 만족하지 못하기 때문에
정다면체가 아니다.
그렇다면 어떻게 생긴 입체를
정다면체라고 할 수 있을까?
우선,
입체가 만들어지기 위해서는
최소한 3개의 면이 만나야
하나의 꼭짓점이 만들어진다는 점과,
각각의 꼭지각
(입체의 꼭짓점에 모인 다각형의 내각)의 합은
360˚보다 작아야 한다는 것을 알고 가야 한다.
[정삼각형이 한 꼭짓점에 3개씩! 모이면]

면이 4개인 정사면체가 된다.
[정삼각형이 한 꼭짓점에 4개씩! 모이면]

면이 8개인 정팔면체가 된다.
[정삼각형이 한 꼭짓점에 5개씩! 모이면]
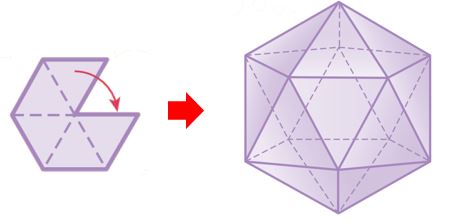
면이 20개인 정이십면체가 된다.
[정삼각형이 한 꼭짓점에 6개 모이면]

꼭짓점에 모이는 각의 합이 360˚가 되어
구부러질 수 없어 입체가 될 수 없다.
따라서,
정삼각형으로 만들 수 있는 정다면체는
정사면체, 정팔면체, 정이십면체가 끝이다.
이제 정사각형으로 만들어보자.
[정사각형이 한 꼭짓점에 3개씩! 모이면]

면이 6개인 정육면체가 된다.
[정사각형이 한 꼭짓점에 4개씩! 모이면]

꼭짓점에 모이는 각의 합이 360˚가 되어
평면이 되기 때문에 입체를 구성할 수 없다.
이제 정오각형을 가지고
정다면체를 만들어보자.
[정오각형이 한 꼭짓점에 3개씩! 모이면]
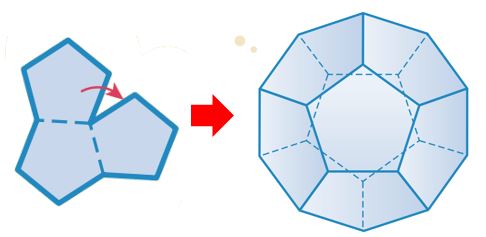
면이 12개인 정십이면체가 된다.
[정오각형이 한 꼭짓점에 4개씩 모이면]

정오각형의 한 내각이 108˚이기 때문에
360˚가 넘어서 입체를 만들 수 없다.
이제 정육각형을 가지고 만들어보자.
[정육각형이 한 꼭짓점에 3개씩! 모이면]

정육각형의 한 내각의 크기가
120˚이기 때문에
꼭짓점에 모인 내각의 합이 360˚가 되어
입체가 만들어 질 수 없다.
즉, 이제 더 이상 정다면체를 만들 수 없다.
따라서 정다면체는

정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체
5개 뿐이다.
이제 정다면체를 그려보자.
이 글의 맨 위쪽을 보면 정다각형은
원에 내접했다.
확장시켜서 생각하면
정다면체는 구에 내접한다.
따라서 원을 틀로 해서
정다면체를 그려보겠다.
정사면체와 정육면체는
쉬우니깐 패스~~
정팔면체부터 그려보자.

1. 실선으로 정삼각형 그리기
2. 점선으로 역삼각형 그리기
3. 각각의 꼭짓점 6개를 실선으로 연결하기
이제 이것은~입체다~생각하며 바라보면
정팔면체를 위에서 내려다본
겨냥도가 등장!!
정십이면체를 그려보자.

1. 실선으로 작은 원에 정오각형을 그리고
정오각형의 꼭짓점에서
원의 중심에서 뻗어나가는 방향으로
큰 원으로 선분 5개를 그린다.
2. 이번에는 안 보이는 모서리를
그려야 하므로 점선으로
거꾸로 된 정오각형을 작은 원에 그리고
원의 중심에서 뻗어나가는 방향으로
정오각형의 꼭짓점에서
큰 원으로 선분 5개를 그린다.
3. 큰 원에 닿아있는 선분의 끝부분을
실선으로 연결한다.
정십이면체 완성!
정이십면체를 그려보자.

1. 실선으로 정삼각형을 그리고
원의 중심에서 뻗어나가는 방향으로
꼭짓점에서 선분 3개 그리기
2. 점선으로 거꾸로 된 정삼각형을 그리고
원의 중심에서 뻗어나가는 방향으로
꼭짓점에서 선분 3개 그리기
3. 실선 정삼각형의 꼭짓점(빨간점)에서
큰 원에 닿아있는 점선 선분의 끝에
두 개의 실선 긋기
4. 점선 정삼각형의 꼭짓점(노란점)에서
큰 원에 닿아있는 실선 선분의 끝에
두 개의 점선 긋기
5. 테두리 꼭짓점 잇기
정이십면체 완성!!