[평면도형]다각형의 내각의 크기의 합

다각형이란,
3개 이상의 선분으로 둘러싸인
평면도형이다.


학생들에게
"삼각형의 내각의 합은?" 이라고
질문하면

단 한명도 빠지지 않고
180˚라고 말한다.


그다음!
"왜??왜? 180˚ 일까?"라는
질문을 하면
당연한걸 왜 물어보시지?라는 얼굴로
나를 쳐다본다.

삼각형의 내각의 합은

왜 180˚일까?

방법1) 평행선을 이용한 방법

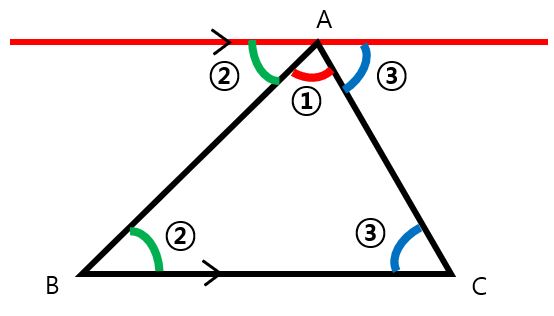
꼭짓점 A를 지나고
삼각형의 밑변과 평행한 선을 그으면
엇각의 성질에 의해
삼각형의 세 내각의 합은 180˚가 된다.



방법2) 풍O중 1학년 4반 이O민 학생의 풀이

삼각형의 내각의 합을 x라고 하자.

삼각형 ABC에서
보조선 AD를 그리자.

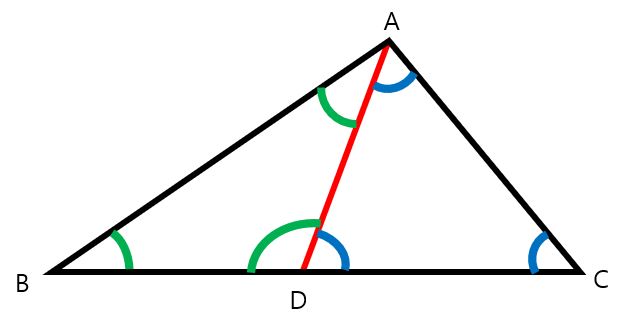
삼각형 ABD의 내각의 합
＋
삼각형 ADC의 내각의 합
─
(각 ADB + 각 ADC)
＝
삼각형 ABC의 내각의 합이다.

식으로 나타내면
x + x - 180˚ = x,
2x - 180˚ =x,
x =180˚

따라서 삼각형의 내각의 합은 180˚이다.

-------------------------------------------------

자! 이제 다각형의 내각의 합의 크기를 구해보자.

각각의 다각형을 한 꼭짓점을 기준으로
삼각형으로 쪼개면 변의 개수보다
2개 적게 쪼개진다.

즉 n각형은 n-2개의
삼각형으로 쪼개진다.




그러면

사각형은
180˚짜리 삼각형 2개로 쪼개지므로
사각형의 내각의 합은
180˚ × 2 = 360˚.


오각형은
180˚짜리 삼각형 3개로 쪼개지므로
오각형의 내각의 합은
180˚ × 3 = 540˚.

육각형은
180˚짜리 삼각형 4개로 쪼개지므로
육각형의 내각의 합은
180˚ × 4 = 720˚.

칠각형은
180˚짜리 삼각형 5개로 쪼개지므로
칠각형의 내각의 합은
180˚ × 5 = 900˚.

팔각형은
180˚짜리 삼각형 6개로 쪼개지므로
팔각형의 내각의 합은
180˚ × 6 = 1080˚이다.

n각형의 내각의 합은

180˚ × (n-2)가 된다.

참고로
정n각형은 모든 내각의 크기가 같기 때문에

이다.